
Concept explainers
(a)
Interpretation:
The probability for the particle having wavefunction
Concept introduction:
For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.
Where,
•
•
•
Answer to Problem 10.27E
The probability for the particle having wavefunction
Explanation of Solution
For the probability of the wavefunction the expression is as follows.
Where,
•
•
•
•
Substitute the values in the above equation as follows.
The above equation is simplified as given below.
The probability for the particle having wavefunction
(b)
Interpretation:
The probability for the particle having wavefunction
Concept introduction:
For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.
Where,
•
•
•
Answer to Problem 10.27E
The probability for the particle having wavefunction
Explanation of Solution
For the probability of the wavefunction the expression is as follows.
Where,
•
•
•
•
Substitute the values in the above equation as follows.
The above equation is simplified as follows.
The probability for the particle having wavefunction
(c)
Interpretation:
The probability for the particle having wavefunction
Concept introduction:
For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.
Where,
•
•
•
Answer to Problem 10.27E
The probability for the particle having wavefunction
Explanation of Solution
For the probability of the wavefunction the expression is as follows.
Where,
•
•
•
•
Substitute the values in the above equation as follows.
The above equation is simplified as follows.
The probability for the particle having wavefunction
(d)
Interpretation:
The probability for the particle having wavefunction
Concept introduction:
For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.
Where,
•
•
•
Answer to Problem 10.27E
The probability for the particle having wavefunction
Explanation of Solution
For the probability of the wavefunction the expression is as follows.
Where,
•
•
•
•
Substitute the values in the above equation as follows.
The above equation is simplified as given below.
The probability for the particle having wavefunction
(e)
Interpretation:
The probability for the particle having wavefunction
Concept introduction:
For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.
Where,
•
•
•
Answer to Problem 10.27E
The probability for the particle having wavefunction
Explanation of Solution
For the probability of the wavefunction the expression is as follows.
Where,
•
•
•
•
Substitute the values in the above equation as follows.
The above equation is simplified as follows.
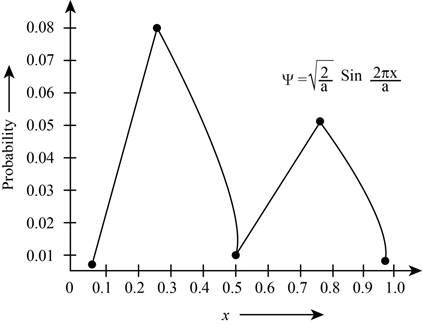
The plot the probabilities versus

Figure 1
The plot shows the probability for the given wave function. According to this plot, the probability of finding the particle is maximum in the range of
The probability for the particle having wavefunction
Want to see more full solutions like this?
Chapter 10 Solutions
EBK PHYSICAL CHEMISTRY
- Synthesize N-Methylcyclohexylamine from cyclohexanol using the necessary organic or inorganic reagents. Draw the structures of the compounds.arrow_forwardSynthesize N-Methylcyclohexylamine from cyclohexanol using the necessary organic or inorganic reagents. Draw the structures of the compounds.arrow_forwardIf possible, please provide the formula of the compound 3,3-dimethylbut-2-enal.arrow_forward
- Synthesize 1,4-dibromobenzene from acetanilide (N-phenylacetamide) using the necessary organic or inorganic reagents. Draw the structures of the compounds.arrow_forwardIndicate the products obtained by mixing (3-oxo-3-phenylpropyl)triphenylphosphonium bromide with sodium hydride.arrow_forwardWe mix N-ethyl-2-hexanamine with excess methyl iodide and followed by heating with aqueous Ag2O. Indicate the major products obtained.arrow_forward
- Indicate the products obtained by mixing acetophenone with iodine and NaOH.arrow_forwardIndicate the products obtained by mixing 2-Propanone and ethyllithium and performing a subsequent acid hydrolysis.arrow_forwardIndicate the products obtained if (E)-2-butenal and 3-oxo-butanenitrile are mixed with sodium ethoxide in ethanol.arrow_forward
- Question 3 (4 points), Draw a full arrow-pushing mechanism for the following reaction Please draw all structures clearly. Note that this intramolecular cyclization is analogous to the mechanism for halohydrin formation. COH Br + HBr Brarrow_forwardIndicate the products obtained if 2,2-dimethylpropanal and acetaldehyde are mixed with sodium ethoxide in ethanol.arrow_forwardIndicate the products obtained if 2,2-dimethylpropanal and acetaldehyde are reacted with sodium ethoxide in ethanol.arrow_forward
 Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,
Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,
