Chapter 1, Problem 22P

As depicted in Fig. P1.22, a spherical particle settling through a quiescent luid is subject to three forces: the downward force of gravity $\left(F_G\right)$, and the upward forces of buoyancy $\left(F_B\right)$ and drag $\left(F_D\right)$. Both the gravity and buoyancy forces can be computed with Newton's second law with the latter equal to the weight of the displaced fluid. For laminar low, the drag force can be computed with Stokes's law,

$F_D=3\pi \mu dv$

where $\mu =$ the dynamic viscosity of the fluid $\left(N{\text{ s/m}}^{\text{2}}\right)$, $d=$ the particle diameter (m), and $v=$ the particle's settling velocity (m/s). Note that the mass of the particle can be expressed as the product of the particle's volume and density ${\rho }_s\left({\text{kg/m}}^{\text{3}}\right)$ and the mass of the displaced fluid can be computed as the product of the particle's volume and the fluid's density $\rho \left({\text{kg/m}}^{\text{3}}\right)$. The volume of a sphere is $\pi d^3\text{/}6$. In addition, laminar low corresponds to the case where the dimension- less Reynolds number, Re, is less than 1, where $\text{Re}=\rho dv\text{/}\mu$.

(a) Use a force balance for the particle to develop the differential equation for $dv\text{/}dt$ as a function of $d,\rho ,{\rho }_s,\text{ and }\mu$.

(b) At steady-state, use this equation to solve for the particle's terminal velocity.

(c) Employ the result of (b) to compute the particle's terminal velocity in m/s for a spherical silt particle settling in water:

$d=10\text{μ}\text{.m},\rho =1g{\text{/cm}}^{\text{3}},{\rho }_s=2.65{\text{g/cm}}^{\text{3}},\text{and }\mu =0.014g\text{/}\left(\text{cm}\cdot \text{s}\right)$.

(d) Check whether low is laminar.

(e) Use Euler's method to compute the velocity from $t=0\text{ to }{2}^{-15}\text{ s}$ with $\Delta t=2^{-18}\text{ s}$ given the parameters given previously along with the initial condition: $v\left(0\right)=0$.

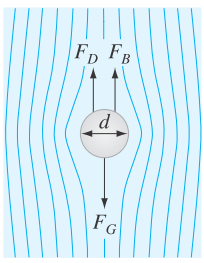
FIGURE P1.22

To determine

The differential equation for $\frac{dv}{dt}$ as a function of $d,\rho ,{\rho }_s\text{ and }\mu$ if the drag force is given as $F_D=3\pi \mu dv$ and the Reynolds number $\mathrm{Re}=\frac{\rho dv}{\mu }$ is less than 1.

Answer to Problem 22P

Solution:

The differential equation for $\frac{dv}{dt}$ as a function of $d,\rho ,{\rho }_s\text{ and }\mu$ is, $\frac{dv}{dt}=g\left(1-\frac{\rho }{{\rho }_s}\right)-\frac{18\mu }{{\rho }_s{d}^2}v$.

Explanation of Solution

Given Information:

The drag force is given as $F_D=3\pi \mu dv$ and the Reynolds number is given as $\mathrm{Re}=\frac{\rho dv}{\mu }$.

Where, $\mu$ is the dynamic viscosity of the fluid $\left(Ns/m^2\right)$, v is the particle settling velocity and d is the particle diameter.

The mass of the particle,

$m=\text{ particle volume}\times \text{density }{\rho }_s$

The mass of the displaced fluid,

$m_f=\text{ particle volume}\times \text{ fluid density }\rho$

The volume of sphere is $\frac{\pi d^3}{6}$.

The figure,

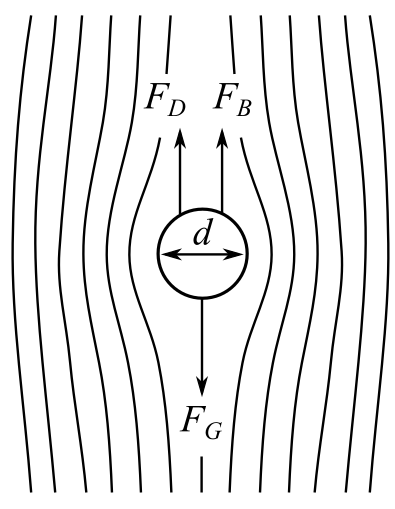
From the provided figure, the drag force and buoyancy force are against the gravitational force.

Therefore, the force balance on the sphere is given as,

$F=F_{\text{gravity}}-F_{\text{buoyancy}}-F_{\text{drag}}$

Here,

$\begin{array}{c}F=ma\\ =m\frac{dv}{dt}\end{array}$

And,

$F_{\text{gravity}}=mg$

And,

$\begin{array}{c}{F}_{\text{buoyancy}}=m_{f}g\\ =\rho Vg\end{array}$

And,

$F_{\text{drag}}=3\pi \mu dv$

Thus, the force balance on the sphere is,

$m\frac{dv}{dt}=mg-\rho Vg-3\pi \mu dv$

Divide the both sides of the above equation by m,

$\begin{array}{c}\frac{dv}{dt}=\frac{mg}{m}-\frac{\rho Vg}{m}-\frac{3\pi \mu dv}{m}\\ =g-\frac{\rho Vg}{m}-\frac{3\pi \mu dv}{m}\end{array}$

Now, the mass of the particle $m=V{\rho }_s$.

Substitute $m=V{\rho }_s$ in the above equation gives,

$\begin{array}{c}\frac{dv}{dt}=g-\frac{\rho Vg}{{\rho }_{s}V}-\frac{3\pi \mu dv}{{\rho }_{s}V}\\ =g-\frac{\rho g}{{\rho }_s}-\frac{3\pi \mu dv}{{\rho }_{s}V}\end{array}$

The volume of the sphere is $\frac{\pi d^3}{6}$.

Substitute $V=\frac{\pi d^3}{6}$ in the above equation,

$\begin{array}{c}\frac{dv}{dt}=g-\frac{\rho g}{{\rho }_s}-\frac{3\pi \mu dv}{{\rho }_s\left(\frac{\pi d^3}{6}\right)}\\ =g\left(1-\frac{\rho }{{\rho }_s}\right)-\frac{18\mu v}{{\rho }_s{d}^2}\end{array}$

Hence, the differential equation for $\frac{dv}{dt}$ is, $\frac{dv}{dt}=g\left(1-\frac{\rho }{{\rho }_s}\right)-\frac{18\mu }{{\rho }_s{d}^2}v$.

To determine

The particle’s terminal velocity at the steady state by the use of the differential equation $\frac{dv}{dt}=g\left(1-\frac{\rho }{{\rho }_s}\right)-\frac{18\mu }{{\rho }_s{d}^2}v$.

Answer to Problem 22P

Solution:

The particle’s terminal velocity at the steady state is $v=\frac{g}{18\mu }\left({\rho }_s-\rho \right)d^2$.

Explanation of Solution

Given Information:

The differential equation $\frac{dv}{dt}=g\left(1-\frac{\rho }{{\rho }_s}\right)-\frac{18\mu }{{\rho }_s{d}^2}v$.

At the steady state, the change in the velocity is zero. Therefore,

$0=g\left(1-\frac{\rho }{{\rho }_s}\right)-\frac{18\mu }{{\rho }_s{d}^2}v$

Now, solve the above equation for particle’s terminal velocity v as below,

$\begin{array}{c}0=g\left(1-\frac{\rho }{{\rho }_s}\right)-\frac{18\mu }{{\rho }_s{d}^2}v\\ \frac{18\mu }{{\rho }_s{d}^2}v=g\left(1-\frac{\rho }{{\rho }_s}\right)\\ v=g\left(1-\frac{\rho }{{\rho }_s}\right)\left(\frac{{\rho }_s{d}^2}{18\mu }\right)\\ =\frac{g}{18\mu }\left(1\times {\rho }_s-\frac{\rho }{{\rho }_s}\times {\rho }_s\right)d^2\end{array}$

Simplify furthermore,

$v=\frac{g}{18\mu }\left({\rho }_s-\rho \right)d^2$

Hence, the particle’s terminal velocity at the steady state is, $v=\frac{g}{18\mu }\left({\rho }_s-\rho \right)d^2$.

To determine

To calculate: The value of particle’s terminal velocity in m/secif the particle’s terminal velocity is given as $v=\frac{g}{18\mu }\left({\rho }_s-\rho \right)d^2$.

Answer to Problem 22P

Solution:

The value of particle’s terminal velocity in m/sec is $6.4232\times {10}^{-5}\text{ m/s}$.

Explanation of Solution

Given Information:

The particle’s terminal velocity is given as $v=\frac{g}{18\mu }\left({\rho }_s-\rho \right)d^2$.

The values,

$\begin{array}{l}d=10\text{ μm}\\ \rho =1{\text{ g/cm}}^{\text{3}}\\ {\rho }_s=2.65{\text{ g/cm}}^{\text{3}}\\ \mu =0.014\text{ g/cm}\times \text{sec}\end{array}$

Formula used:

The conversions,

$\begin{array}{c}1\text{ μm}={10}^{-6}\text{m}\\ \text{1 cm}={10}^{-2}\text{m}\\ \text{1g}={10}^{-3}\text{kg}\end{array}$

Calculation:

The particle’s terminal velocity at the steady state is, $v=\frac{g}{18\mu }\left({\rho }_s-\rho \right)d^2$.

Convert the provided values in to the required units as below,

$\begin{array}{c}d=10\text{ μm}\\ =10\times {10}^{-6}\text{m}\\ {\text{=10}}^{-5}\text{m}\end{array}$

And,

$\begin{array}{c}\rho =1\frac{\text{g}}{{\text{cm}}^{\text{3}}}\\ =1\frac{{\text{10}}^{-3}\text{ kg}}{{\left({10}^{-2}\text{m}\right)}^3}\\ =\frac{\text{1}\times {\text{10}}^{-3}}{{10}^{-6}}\frac{\text{kg}}{{\text{m}}^{\text{3}}}\\ ={10}^3\frac{\text{kg}}{{\text{m}}^{\text{3}}}\end{array}$

And,

$\begin{array}{c}{\rho }_s=2.65\frac{\text{kg}}{{\text{cm}}^{\text{3}}}\\ =2.65\frac{{\text{10}}^{-3}\text{kg}}{{\left({10}^{-2}\text{m}\right)}^{\text{3}}}\\ =2.65\frac{{\text{10}}^{-3}\text{kg}}{{10}^{-6}{\text{m}}^{\text{3}}}\\ =2.65\times {10}^3\frac{\text{kg}}{{\text{m}}^{\text{3}}}\end{array}$

And,

$\begin{array}{c}\mu =0.014\frac{\text{g}}{\text{cm}\cdot \text{sec}}\\ \text{=}0.014\frac{{\text{10}}^{-3}\text{kg}}{{\text{10}}^{-2}\text{m}\cdot \text{sec}}\\ \text{=}0.014\times {\text{10}}^{-1}\frac{\text{kg}}{\text{m}\cdot \text{sec}}\\ =0.0014\frac{\text{kg}}{\text{m}\cdot \text{sec}}\end{array}$

Substitute $d={\text{10}}^{-5}\text{m}$, $\rho ={\text{10}}^3\frac{\text{kg}}{{\text{m}}^{\text{3}}}$, ${\rho }_s=2.65\times {10}^3\frac{\text{kg}}{{\text{m}}^{\text{3}}}$ and $\mu =0.0014\frac{\text{kg}}{\text{m}\cdot \text{sec}}$ in the equation of particle’s terminal velocity and solve as below,

$\begin{array}{c}v=\frac{g}{18\mu }\left({\rho }_s-\rho \right)d^2\\ =\frac{9.81}{18\times 0.0014}\left(2.65\times {10}^3-{10}^3\right)\times {\left({10}^{-5}\right)}^2\text{ m/s}\\ \text{=}\frac{9.81}{0.0252}\left[\left(2.65-1\right)\times {10}^3\right]\times {10}^{-10}\text{ m/s}\\ =389.2857\times 1.65\times {10}^{-7}\text{ m/s}\end{array}$

Simplify furthermore,

$\begin{array}{c}v=389.2857\times 1.65\times {10}^{-7}\text{ m/s}\\ =642.32\times {10}^{-7}\text{ m/s}\\ =6.4232\times {10}^{-5}\text{ m/s}\end{array}$

Hence, the value of the particle’s terminal velocity in m/sec is $6.4232\times {10}^{-5}\text{ m/s}$.

To determine

Whether the flow is laminar or not if the Reynolds number is given as $\mathrm{Re}=\frac{\rho dv}{\mu }$.

Answer to Problem 22P

Solution:

The flow is laminar.

Explanation of Solution

Given Information:

The Reynolds number is given as $\mathrm{Re}=\frac{\rho dv}{\mu }$.

The values,

$\begin{array}{l}d=10\text{ μm}\\ \rho =1{\text{ g/cm}}^{\text{3}}\\ v=6.4232\times {10}^{-5}\text{ m/s}\\ \mu =0.014\text{ g/cm}\times \text{sec}\end{array}$

The flow is laminar if the value of Reynolds number is less than 1.

Now, consider the Reynolds number as,

$\mathrm{Re}=\frac{\rho dv}{\mu }$

From part (c),

$\begin{array}{l}d={\text{10}}^{-5}\text{m}\\ \rho ={\text{10}}^3\frac{\text{kg}}{{\text{m}}^{\text{3}}}\end{array}$

And,

$\mu =0.0014\frac{\text{kg}}{\text{m}\cdot \text{sec}}$

Substitute the values $d={10}^{-5}\text{m,}\rho ={\text{10}}^3\frac{\text{kg}}{{\text{m}}^{\text{3}}},v=6.4232\times {10}^{-5}\text{ m/s and }\mu =0.0014\text{ kg/m}\cdot \text{sec}$ in the above equation as below,

$\begin{array}{c}\mathrm{Re}=\frac{\rho dv}{\mu }\\ =\frac{{10}^3\times {10}^{-5}\times 6.4232\times {10}^{-5}}{0.0014}\\ =\frac{6.4232\times {10}^{-7}}{0.0014}\\ =0.4588\times {10}^{-3}\end{array}$

Since, the Reynolds number is less than 1.

Hence, the flow is laminar.

To determine

To calculate: The velocity from $t=0{\text{ to 2}}^{-15}\text{ sec}$ by the Euler’s method with the step size $\Delta t=2^{-18}$ and the initial condition $v\left(0\right)=0$.

Answer to Problem 22P

Solution:

The velocity from $t=0{\text{ to 2}}^{-15}\text{ sec}$ by the Euler’s method is,

t	v	dv/dt
0	0	6.10771
3.8147E-06	2.32991E-05	3.891969
7.6294E-06	3.81457E-05	2.480049
1.1444E-05	4.76064E-05	1.580343
1.5259E-05	5.36349E-05	1.00703
1.9073E-05	5.74764E-05	0.641702
2.2888E-05	5.99243E-05	0.408907
2.6703E-05	6.14842E-05	0.260564
3.0518E-05	6.24782E-05	0.166037

Explanation of Solution

Given Information:

The values,

$\begin{array}{l}d=10\text{ μm}\\ \rho =1{\text{ g/cm}}^{\text{3}}\\ {\rho }_s=2.65{\text{ g/cm}}^{\text{3}}\\ \mu =0.014\text{ g/cm}\times \text{sec}\end{array}$

The initial condition $v\left(0\right)=0$.

Formula used:

Euler’s method for $\frac{dy}{dx}=f\left(x,y\right)$ is,

$y\left(x+h\right)=y\left(x\right)+hf\left(x,y\right)$

Where, h is the step size.

Calculation:

From part (a), the differential equation is,

$\frac{dv}{dt}=g\left(1-\frac{\rho }{{\rho }_s}\right)-\frac{18\mu }{{\rho }_s{d}^2}v$

Convert the provided values in to the standard MKS units as below,

$\begin{array}{c}d=10\text{ μm}\\ =10\times {10}^{-6}\text{m}\\ {\text{=10}}^{-5}\text{m}\end{array}$

And,

$\begin{array}{c}\rho =1\frac{\text{g}}{{\text{cm}}^{\text{3}}}\\ =1\frac{{\text{10}}^{-3}\text{ kg}}{{\left({10}^{-2}\text{m}\right)}^3}\\ =\frac{\text{1}\times {\text{10}}^{-3}}{{10}^{-6}}\frac{\text{kg}}{{\text{m}}^{\text{3}}}\\ ={10}^3\frac{\text{kg}}{{\text{m}}^{\text{3}}}\end{array}$

And,

$\begin{array}{c}{\rho }_s=2.65\frac{\text{kg}}{{\text{cm}}^{\text{3}}}\\ =2.65\frac{{\text{10}}^{-3}\text{kg}}{{\left({10}^{-2}\text{m}\right)}^{\text{3}}}\\ =2.65\frac{{\text{10}}^{-3}\text{kg}}{{10}^{-6}{\text{m}}^{\text{3}}}\\ =2.65\times {10}^3\frac{\text{kg}}{{\text{m}}^{\text{3}}}\end{array}$

And,

$\begin{array}{c}\mu =0.014\frac{\text{g}}{\text{cm}\cdot \text{sec}}\\ \text{=}0.014\frac{{\text{10}}^{-3}\text{kg}}{{\text{10}}^{-2}\text{m}\cdot \text{sec}}\\ \text{=}0.014\times {\text{10}}^{-1}\frac{\text{kg}}{\text{m}\cdot \text{sec}}\\ =0.0014\frac{\text{kg}}{\text{m}\cdot \text{sec}}\end{array}$

Substitute $d={\text{10}}^{-5}\text{m}$, $\rho ={\text{10}}^3\frac{\text{kg}}{{\text{m}}^{\text{3}}}$, ${\rho }_s=2.65\times {10}^3\frac{\text{kg}}{{\text{m}}^{\text{3}}}$ and $\mu =0.0014\frac{\text{kg}}{\text{m}\cdot \text{sec}}$ in the differential equation of particle’s terminal velocity and solve as below,

$\begin{array}{c}\frac{dv}{dt}=g\left(1-\frac{\rho }{{\rho }_s}\right)-\frac{18\mu }{{\rho }_s{d}^2}v\\ =9.81\left(1-\frac{{10}^3}{2.65\times {10}^3}\right)-\frac{18\times 0.0014}{2.65\times {10}^3\times {\left({10}^{-5}\right)}^2}\times v\\ =9.81\left(1-0.3774\right)-0.00951\times {10}^{7}v\\ =6.10771-95100v\end{array}$

The iteration formula for Euler’s method with step size $\Delta t=2^{-18}$ for the above equation is,

$v\left(t+2^{-18}\right)=v\left(t\right)+2^{-18}\left(6.10771-95100v\left(t\right)\right)$

Use excel to find all the iteration with step size $\Delta t=2^{-18}$ from $t=0{\text{ to 2}}^{-15}\text{ sec}$ as below,

Step 1: Name the column A as t and go to column A2 and put 0 then go to column A3and write the formula as,

=A2+2^(-18)

Then, Press enter and drag the column up to the $t=3.0518\times {10}^{-5}$.

Step 2: Now name the column B as v and go to column B2 and write 0 and then go to the column B3 and write the formula as,

=B3+2^(-18)*(6.10771-95100*B3)

Step 3: Press enter and drag the column up to the $t=3.0518\times {10}^{-5}$.

Step 4. Now name the column C as dv/dt and go to column C2 and write the formula as,

=6.10771-95100*B2

Step 5. Press enter and drag the column up to the $t=3.0518\times {10}^{-5}$.

Thus, all the iterations are as shown below,

t	v	dv/dt
0	0	6.10771
3.8147E-06	2.32991E-05	3.891969
7.6294E-06	3.81457E-05	2.480049
1.1444E-05	4.76064E-05	1.580343
1.5259E-05	5.36349E-05	1.00703
1.9073E-05	5.74764E-05	0.641702
2.2888E-05	5.99243E-05	0.408907
2.6703E-05	6.14842E-05	0.260564
3.0518E-05	6.24782E-05	0.166037