Chapter 1, Problem 1RE

In Problems 1–3, use point-by-point plotting to sketch the graph of each equation.

1. y = 5 − x²

To determine

To sketch: The graph of the equation $y=5-x^2$ by using point-by-point plotting method.

Explanation of Solution

The given equation is $y=5-x^2$.

Choose integer values for x and find the corresponding ordered pairs of $y=5-x^2$.

The value of y for different x values for the equation $y=5-x^2$ is shown below in Table 1.

x	$y=5-x^2$
–2	1
–1	4
0	5
1	4
2	1

Table 1

Use the above ordered pairs to sketch the graph of the equation $y=5-x^2$ as shown below in Figure 1.

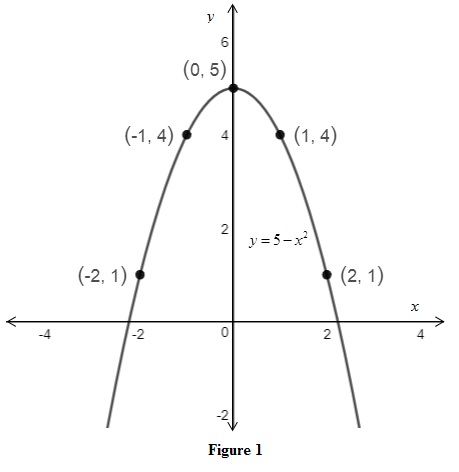
From Figure 1, it is observed that the graph of the equation $y=5-x^2$ represents a downward parabola. Every point on this parabola is a solution of the quadratic equation $y=5-x^2$.