Chapter 1, Problem 163E

(a)

To determine

To find: The graphical and numerical summary of the provided data of number of users of internet per 100 people in the year 2010 (Users2010) and to find the numerical summaries of the provided data.

Solution: The obtained histogram indicates that distribution of the data is right skewed. According to the numerical summary, mean of the data is 35.64, minimum value of the data is 0.21, first quartile is 10.31, the median is 31.40, third quartile is 55.65 and the maximum value is 95.63.

Explanation of Solution

Given: The data of number of users of internet per 100 people (Users2010) is provided in the question.

Country Name	Users2010	Users2011
Afghanistan	3.65	4.58
Albania	45.00	49.00
Algeria	12.50	14.00
Andorra	81.00	81.00
Angola	10.00	14.78
Antigua and Barbuda	80.00	82.00
Argentina	40.00	47.70
Aruba	42.00	57.07
Australia	75.89	78.95
Austria	75.20	79.75
Azerbaijan	46.68	50.75
Bahamas, The	43.00	65.00
Bahrain	55.00	77.00
Bangladesh	3.70	5.00
Barbados	70.20	71.77
Belarus	32.15	39.96
Belgium	73.74	76.20
Benin	3.13	3.50
Bermuda	85.13	88.85
Bhutan	13.60	21.00
Bolivia	22.40	30.00
Bosnia and Herzegovina	52.00	60.00
Botswana	6.00	7.00
Brazil	40.65	45.00
Brunei Darussalam	53.00	56.00
Bulgaria	45.98	50.80
Burkina Faso	2.40	3.00
Burundi	1.00	1.11
Cambodia	1.26	3.10
Cameroon	4.30	5.00
Canada	80.04	82.68
Cape Verde	30.00	32.00
Cayman Islands	66.00	69.47
Central African Republic	2.00	2.20
Chad	1.70	1.90
Chile	45.00	53.89
China	34.39	38.40
Colombia	36.50	40.40
Comoros	5.10	5.50
Congo, Dem. Rep.	0.72	1.20
Congo, Rep.	5.00	5.60
Costa Rica	36.50	42.12
Cote d'Ivoire	2.10	2.20
Croatia	60.12	70.53
Cuba	15.90	23.23
Cyprus	52.99	57.68
Czech Republic	68.64	72.89
Denmark	88.76	89.98
Djibouti	6.50	7.00
Dominica	47.45	51.31
Dominican Republic	31.40	35.50
Ecuador	29.03	31.40
Egypt, Arab Rep.	30.20	35.62
El Salvador	15.90	17.69
Eritrea	5.40	6.20
Estonia	74.15	76.53
Ethiopia	0.75	1.10
Faeroe Islands	75.20	80.73
Fiji	20.00	28.00
Finland	86.91	89.33
France	77.28	76.77
French Polynesia	49.00	49.00
Gabon	7.23	8.00
Gambia, The	9.20	10.87
Georgia	26.29	35.28
Germany	82.53	83.44
Ghana	9.55	14.11
Greece	44.57	53.40
Greenland	63.85	64.62
Guatemala	10.50	11.73
Guinea	1.00	1.30
Guinea-Bissau	2.45	2.67
Guyana	29.90	32.00
Honduras	11.09	15.90
Hong Kong SAR, China	71.85	75.03
Hungary	52.91	58.97
Iceland	95.63	96.62
India	7.50	10.07
Indonesia	10.92	18.00
Iran, Islamic Rep.	16.00	21.00
Iraq	2.47	4.95
Ireland	69.78	77.48
Israel	65.68	68.17
Italy	53.74	56.82
Jamaica	28.07	31.99
Japan	77.65	78.71
Jordan	27.83	35.74
Kazakhstan	31.03	44.04
Kenya	14.00	28.00
Kiribati	9.07	10.00
Korea, Rep.	81.62	81.46
Kuwait	61.40	74.20
Kyrgyz Republic	18.02	19.58
Lao PDR	7.00	9.00
Latvia	68.82	72.43
Lebanon	43.68	52.00
Lesotho	3.86	4.22
Liberia	2.30	3.00
Libya	14.00	17.00
Liechtenstein	80.00	85.00
Lithuania	62.82	67.17
Luxembourg	90.71	90.70
Macao SAR, China	53.80	58.00
Macedonia, FYR	51.90	56.70
Madagascar	1.70	1.90
Malawi	2.26	3.33
Malaysia	56.30	61.00
Maldives	28.30	34.00
Mali	1.90	2.00
Malta	63.08	69.03
Mauritania	4.00	4.50
Mauritius	28.73	35.51
Mexico	31.05	36.15
Moldova	32.40	37.85
Mongolia	12.90	20.00
Montenegro	37.50	40.00
Morocco	49.00	51.00
Mozambique	4.17	4.30
Myanmar	0.25	0.98
Namibia	11.60	12.00
Nepal	7.93	9.00
Netherlands	90.71	92.13
New Caledonia	42.66	51.17
New Zealand	83.01	86.18
Nicaragua	10.00	10.60
Niger	0.83	1.30
Nigeria	24.00	28.43
Norway	93.27	93.45
Oman	62.00	68.00
Pakistan	8.00	9.00
Panama	40.10	42.70
Papua New Guinea	1.28	2.00
Paraguay	19.80	23.90
Peru	34.77	36.50
Philippines	25.00	29.00
Poland	62.47	65.02
Portugal	51.28	55.57
Puerto Rico	45.63	48.50
Qatar	81.60	86.20
Romania	40.02	44.12
Russian Federation	43.31	49.31
Rwanda	8.00	7.00
Sao Tome and Principe	18.75	20.16
Saudi Arabia	41.00	47.50
Senegal	16.00	17.50
Serbia	45.56	47.19
Seychelles	41.00	43.61
Singapore	71.14	75.06
Slovak Republic	76.16	74.87
Slovenia	69.35	71.40
Solomon Islands	5.00	6.00
South Africa	18.05	20.95
Spain	65.81	67.92
Sri Lanka	12.12	15.13
St. Lucia	40.06	42.01
St. Vincent and the Grenadines	38.50	43.01
Suriname	31.59	32.00
Swaziland	12.41	20.43
Sweden	90.01	90.88
Switzerland	82.17	82.99
Syrian Arab Republic	20.66	22.44
Tajikistan	11.55	13.03
Tanzania	11.00	12.00
Thailand	22.40	23.70
Timor-Leste	0.21	0.88
Togo	3.00	3.50
Tonga	16.00	25.00
Trinidad and Tobago	48.50	55.20
Tunisia	36.56	38.81
Turkey	39.82	42.10
Turkmenistan	3.00	5.00
Tuvalu	25.00	30.00
Uganda	12.50	13.01
Ukraine	23.09	30.25
United Arab Emirates	68.00	70.00
United Kingdom	77.75	81.71
United States	74.25	78.24
Uruguay	46.57	51.57
Uzbekistan	19.22	28.57
Venezuela, RB	37.56	40.44
Vietnam	30.97	35.45
West Bank and Gaza	43.44	56.82
Yemen, Rep.	12.35	14.91
Zambia	10.13	11.50
Zimbabwe	11.50	15.70

Graph: To draw the histogram of the provided data, below mentioned steps are followed in Minitab.

Step 1: Enter the data into Minitab worksheet.

Step 2: Go to Graph, select Histogram and select simple and click OK.

Step 3: Select the data variable column of “Users2010” and click on Scale.

Step 4: Check minor ticks under Y Scale Low and X Scale Low and then click OK.

The obtained histogram is as follows:

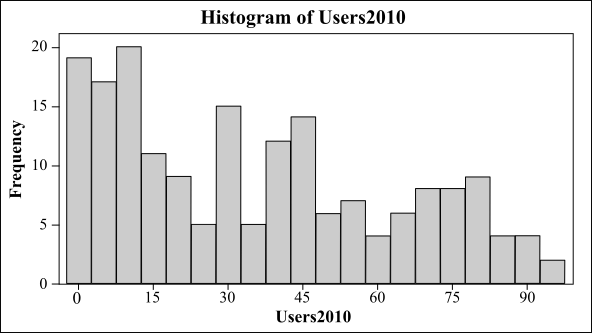
Calculation: Use the following steps in Minitab to find the numerical summary for percent users of internet per 100 people.

Step 1. Go to stat option then click on Basis statistics and then choose Display Descriptive Statistics.

Step 2. Click on statistics and check minor ticks under Mean, First quartile, Median, Third quartile, Minimum and Maximum.

The numerical summary for percent of users of internet per 100 people in the year 2010 is as follows:

$\begin{array}{l}\text{Varible Mean Minimum Q1 Median Q3 Maximum}\\ \text{SmokeEveryDay 35}\text{.64 0}\text{.21 10}\text{.31 31}\text{.40 55}\text{.65 95}\text{.63}\end{array}$

Interpretation: The obtained histogram of the data is plotted and it shows that the data is normal and is right skewed. The mean of the data is 35.64, minimum value of the data is 0.21, first quartile is 10.31, the median is 31.40, third quartile is 55.65 and the maximum value is 95.63.

(b)

To determine

To find: The change in number of users per 100 people from 2010 to 2011 and to analyze the changes.

Answer to Problem 163E

Solution: The minimum value of the data is $-1.285$, first quartile is $0.996$, the median is $2.570$, third quartile is $4.811$ and the maximum value is 22.000.

Explanation of Solution

Calculation:

Use the following steps in Minitab to find the change in number of users per 100 people from 2010 to 2011.

Step 1. Go to Calc then click on Calculator and enter change in Store result option and enter the formula ‘User2011’-‘User2010’ in the expression option and then click OK.

Step 2. Go to Stat option then click on Basis Statistics and then choose Display Descriptive Statistics.

Step 3. Click on Statistics and check minor ticks under First quartile, Median, Third quartile, Minimum and Maximum.

The numerical summary for change in number of users per 100 people from 2010 to 2011 is as follows:

$\begin{array}{l}\text{Varible Minimum Q1 Median Q3 Maximum}\\ \text{SmokeEveryDay }-1.285\text{ 0}\text{.996 }2.570\text{ 4}\text{.811 22}\text{.000}\end{array}$

To draw the histogram of the provided data, below mentioned steps are followed in Minitab.

Step 1: Enter the data into Minitab worksheet.

Step 2: Go to Graph, select Histogram and select simple and click OK.

Step 3: Select the data variable column of “change” and click on Scale.

Step 4: Check minor ticks under Y Scale Low and X Scale Low and then click OK.

The obtained histogram is as follows:

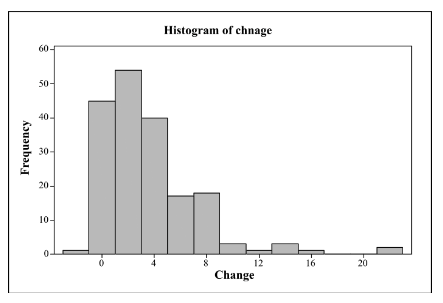
Interpretation: The obtained histogram of the data is plotted and it shows that the data is normal and is left skewed. The minimum value of the data is $-22.00$, first quartile is $-4.811$, the median is $-2.570$, third quartile is $-0.996$ and the maximum value is 1.285.

(c)

To determine

To find: The percent change in number of users per 100 people from 2010 to 2011 and to analyze the changes.

Answer to Problem 163E

Solution: The minimum value of the data is $-12.50$, first quartile is $5.58$, the median is $10.75$, third quartile is $20.70$ and the maximum value is 327.32.

Explanation of Solution

Calculation: Use the following steps in Minitab to find the percent change in number of users per 100 people from 2010 to 2011.

Step 1. Go to Calc then click on Calculator and enter % change in Store result option and enter the formula $\left(‘\text{User}2011’-‘\text{User}2010’\right)*100/\text{User}2010$ in the expression option and then click OK.

Step 2. Go to stat option then click on Basis statistics and then choose Display Descriptive Statistics.

Step 3. Click on statistics and check minor ticks under First quartile, Median, Third quartile, Minimum and Maximum.

The numerical summary for change in number of users per 100 people from 2010 to 2011 is as follows:

$\begin{array}{l}\text{Varible Minimum Q1 Median Q3 Maximum}\\ \text{SmokeEveryDay }-12.50\text{ 5}\text{.58 10}\text{.75 20}\text{.70 327}\text{.32}\end{array}$

To draw the histogram of the provided data, below mentioned steps are followed in Minitab.

Step 1: Enter the data into Minitab worksheet.

Step 2: Go to Graph, select Histogram and select simple and click OK.

Step 3: Select the data variable column of “%change” and click on Scale.

Step 4: Check minor ticks under Y Scale Low and X Scale Low and then click OK.

The obtained histogram is as follows:

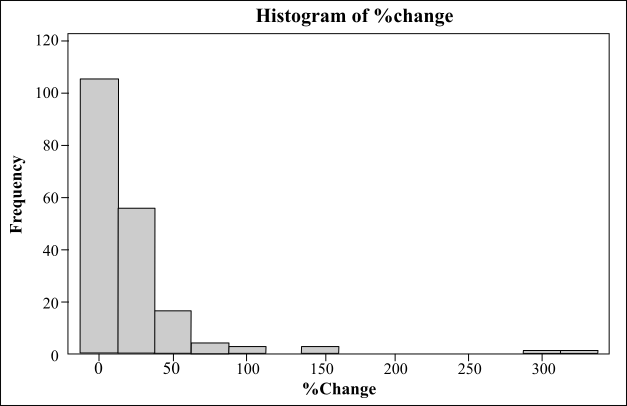
Interpretation: The obtained histogram of the data is plotted and it shows that the data is right skewed. The minimum value of the data is $-12.50$, first quartile is $5.58$, the median is $10.75$, third quartile is $20.70$ and the maximum value is 327.32.

(d)

To determine

The summary to the analysis from part (a) to (c) and to compare between the change and percent change in number of users per 100 people from 2010 to 2011

Answer to Problem 163E

Solution: Internet utilization has considerably expanded from 2010 to 2011 and the data for internet use in the year 2010 is right skewed.

Explanation of Solution

The data for internet use in the year 2010 is right skewed. The change in internet use from 2010 to 2011 and the percent change are also right skewed. Moreover, there is a gap between the percentage change and it is obtained from the histogram. For every one of the data, numerical summary appears the most ideal approach to depict the distribution. Internet utilization has considerably expanded from 2010 to 2011.