You have a finicky parrot and a bag of four kinds of parrot treats. This bag has 6 sweet potato treats, 8 beet treats, 7 peanut butter treats, and 9 berry treats. Today, your parrot has decided it will only eat berry treats, so you keep pulling a treat from the bag and offering it to your parrot. If it doesn’t eat it, you put the treat back, mix the treats around, and offer your parrot another at random. (a) What is the probability that the first treat your parrot accepts is the fourth one you offer? (b) What is the probability that your parrot won’t accept a treat until after your second offering?
You have a finicky parrot and a bag of four kinds of parrot treats. This bag has 6 sweet potato treats, 8 beet treats, 7 peanut butter treats, and 9 berry treats. Today, your parrot has decided it will only eat berry treats, so you keep pulling a treat from the bag and offering it to your parrot. If it doesn’t eat it, you put the treat back, mix the treats around, and offer your parrot another at random.
(a) What is the
(b) What is the probability that your parrot won’t accept a treat until after your second offering?
Consider an infinite sequence of Bernoulli trials with probability of obtaining a success in a trial = p
Now, if X denote the no. of failures preceding the first success then, X~Geometric(p) where the pdf of X is given by,
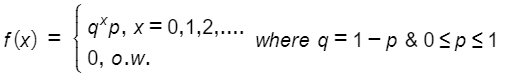
Again let us consider another variable Y denoting the no. of trials in order to obtain the first success then Y~Geometric(p) whose pdf is given by,
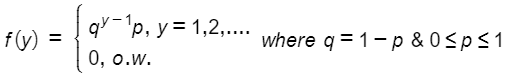
Step by step
Solved in 3 steps with 4 images









