Homework Help is Here – Start Your Trial Now!
Math
Probability
You are a member of a data science team of a major cancer specializing hos- pital. To plan resources (beds, personnel etc.) one of the metrics you are asked to estimate is the probability of a patient having cancer given a positive cancer screenings test result. Your manager told you to call this probability p(cancers+) has given you the data you need: 1. 1% of women have breast cancer (and therefore 99% do not). 2. 80% of mammograms detect breast cancer when it is there (and therefore 20% miss it). 3. 9.6% of mammograms detect breast cancer when it's not there (and there- fore 90.4% correctly return a negative result). While asking around for anyone that has done this before, a colleague of yours is giving you several hints: "Luckily, your manager gave you the prior probability p(cancer)" • "Just use the Bayes rule p(ab) = p(ba)p(a)/p(b) and you will be OK".

You are a member of a data science team of a major cancer specializing hos- pital. To plan resources (beds, personnel etc.) one of the metrics you are asked to estimate is the probability of a patient having cancer given a positive cancer screenings test result. Your manager told you to call this probability p(cancers+) has given you the data you need: 1. 1% of women have breast cancer (and therefore 99% do not). 2. 80% of mammograms detect breast cancer when it is there (and therefore 20% miss it). 3. 9.6% of mammograms detect breast cancer when it's not there (and there- fore 90.4% correctly return a negative result). While asking around for anyone that has done this before, a colleague of yours is giving you several hints: "Luckily, your manager gave you the prior probability p(cancer)" • "Just use the Bayes rule p(ab) = p(ba)p(a)/p(b) and you will be OK".

A First Course in Probability (10th Edition)
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
See similar textbooks
icon
Related questions
Question

Please Help ASAP!!!

 

You are a member of a data science team at a major cancer-specializing hospital. To plan resources (beds, personnel, etc.), one of the metrics you are asked to estimate is the probability of a patient having cancer given a positive cancer screening \( s \) test result. Your manager told you to call this probability \( p(\text{cancer}|s=+) \) and has given you the data you need: 1. 1% of women have breast cancer (and therefore 99% do not). 2. 80% of mammograms detect breast cancer when it is there (and therefore 20% miss it). 3. 9.6% of mammograms detect breast cancer when it’s not there (and therefore 90.4% correctly return a negative result). While asking around for anyone that has done this before, a colleague of yours is giving you several hints: - “Luckily, your manager gave you the prior probability \( p(\text{cancer}) \).” - “Just use the Bayes rule \( p(a|b) = p(b|a)p(a)/p(b) \) and you will be OK.”
Transcribed Image Text:You are a member of a data science team at a major cancer-specializing hospital. To plan resources (beds, personnel, etc.), one of the metrics you are asked to estimate is the probability of a patient having cancer given a positive cancer screening \( s \) test result. Your manager told you to call this probability \( p(\text{cancer}|s=+) \) and has given you the data you need: 1. 1% of women have breast cancer (and therefore 99% do not). 2. 80% of mammograms detect breast cancer when it is there (and therefore 20% miss it). 3. 9.6% of mammograms detect breast cancer when it’s not there (and therefore 90.4% correctly return a negative result). While asking around for anyone that has done this before, a colleague of yours is giving you several hints: - “Luckily, your manager gave you the prior probability \( p(\text{cancer}) \).” - “Just use the Bayes rule \( p(a|b) = p(b|a)p(a)/p(b) \) and you will be OK.”
Expert Solution
Step 1

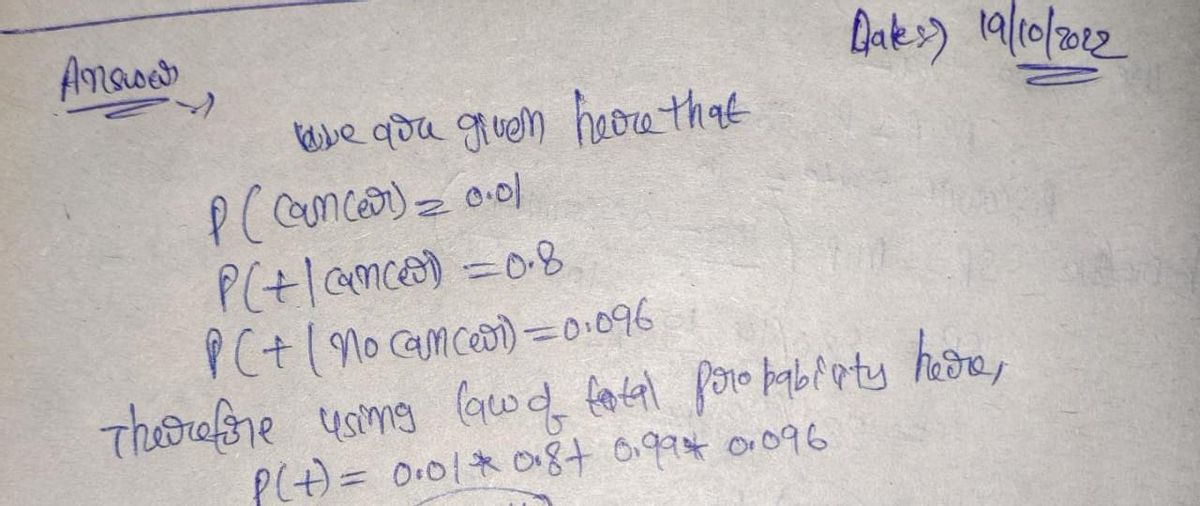
Probability homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer