You and a group of friends wish to start a company. You have an idea, and you are co startup incubators to apply to. (Start up incubators hold classes and help startups to venture capitalists and network with one another) Assume funding is normally distrib

(a). Test whether the success ratios significantly different:
Let p1 be the population proportion of companies of incubator-A survive.
Let p2 be the population proportion of companies of incubator-B survive.
Let (p1– p2) be the difference between the population proportions of companies that survive for company-A and company-B.
The researcher’s objective is to test, whether the success ratios significantly different.
The hypotheses are given below:
Null hypothesis:
H0 : p1 = p2
That is, there is no significant difference between the population proportion of successful companies of incubator-A and the population proportion of successful companies of incubator-B.
Alternative hypothesis:
Ha : p1 ≠ p2 (Two tailed test)
That is, there is a significant difference between the population proportion of successful companies of incubator-A and the population proportion of successful companies of incubator-B.
Obtain the pooled estimate of proportion:
Here, p1^ = 0.7 and p2^2 = 0.4.
Here, n1 = 28 n2 = 20.
The pooled estimate of proportion is obtained as 0.575 from the calculation given below:
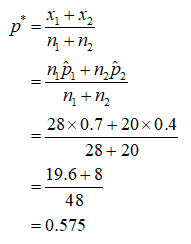
Obtain the test statistic value:
Here, (p1– p2) = 0, p1-hat = 0.7, p2-hat = 0.4, n1 = 28, n2 = 20.
The test statistic value is obtained as 2.07 from the calculation given below:
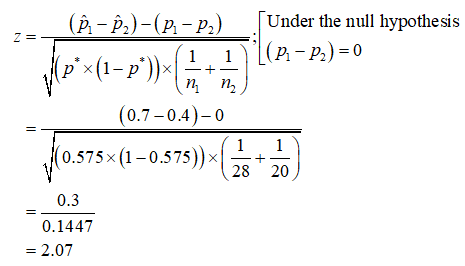
Obtain the critical value for the given situation:
The level of significance is α = 0.01.
The critical value corresponding to the given situation is obtained as z(α/2) = ±2.58 from the calculation given below:

Decision rule:
Denote z as test statistic value and z(α/2) as the critical value.
Decision rule based on critical approach:
If z ≤ –z(α/2) (or) z ≥ z(α/2), then reject the null hypothesis H0.
If –z(α/2) < z < z(α/2), then fail to reject the null hypothesis H0.
Conclusion:
Conclusion based on critical value approach:
The test statistic value is 2.07 and critical value is ±2.58
Here, –z(α/2) < z < z(α/2). That is, -2.58 (= z(α/2)) < 2.07 (=z) < 2.58 (= z(α/2)).
By the rejection rule, fail to reject the null hypothesis H0.
Hence, there is no significant difference between the population proportion of successful companies of incubator-A and the population proportion of successful companies of incubator-B.
Hence, the success ratios are not significantly different.
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 4 images




