x=J_y=K z=L Suppose G(J, K,L)= < 2 cos L, 6KL + eK,3K² - 2J sin L > • Then show: Gis conservative; find a potential function for G. By the Fundamental Theorem for Line Integrals: Then, evaluate TT Tr SdP such that A is path defined by P (r) = < −5r + 4, 2rer−¹, COS A 3 > for r = [0,1]

x=J_y=K z=L Suppose G(J, K,L)= < 2 cos L, 6KL + eK,3K² - 2J sin L > • Then show: Gis conservative; find a potential function for G. By the Fundamental Theorem for Line Integrals: Then, evaluate TT Tr SdP such that A is path defined by P (r) = < −5r + 4, 2rer−¹, COS A 3 > for r = [0,1]

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Q: e) S(secx + cotx)* dx 2.

A: To evaluate the given integral

Q: Find the area in the first quadrant that is inside the circle r = 4 sin 0 and outside the lemniscate…

A: We need to find area. NOTE - As per our guidelines we can solve one question so please upload…

Q: Evaluate the integral: Hint: Integrate by parts. Olet u=x², du=2xdx, dv=cosxdx, v= sinx [x²cosxdx =…

A: We have to evaluate the integral.

Q: Without finding a potential function, determine if G : , 2y^x is conservative.

Q: Find a potential function for F. f(x,y,z) =

Q: So(by² i + x }) · dř =

Q: let X~beta(a,b). find m.g.f ofY=ln| 1-x

Q: Given the information on the image, how do I show that F is conservative, and how do I find the…

A: The given vector filed function is Fxy=2xy+y2x2+2xy. If F=px,yqx,y be a vector field on an open…

Q: 13. Integrate: S(sec³ 0 tan 0 - sec 0 tan³ 0)d0 A. In sec 0 + C В. In sin @ + С C. sec 0 + C D. sin…

Q: Exercises (13): Evaluate the following integrals 1. x²e*dx

A: As per bertleby guide line I have to solve the first question only, please resubmit the other…

Q: The differential of the function f(x,t)= e cos(2 tt) at the point (x,t)= (0,1) is given by -2dx +2…

A: Topic- Application of derivatives

Q: Problem 1. (Line Integration) Consider the curve c(t) = (e*, e-t) with 0 <t<1 and the vector field…

A: Given:

Q: consists of y = 4-x and straight line from (-2,0) to (2,0). Sketch the curve C. 64 ans: 3

Q: Ex: Find the F.T. of the rectangular pulse (gate function). f(t) = A rect ( =) = ATT (t/), I is the…

A: Hint: We need to find the Fourier transformation of f(t)=A rect(tτ)

Q: Calculate the gradient of the following function fox, y) = (x – 2)^3 sin y, at (0,0]

Q: Find a potential function for F(x, y, z) = :yi+xj+xzk or prove none exists.

Q: Integrate f(z) = (7)° counterclockwise around the unit circle, using Cauchy's integral theorem if…

A: using cauchy residue theorem to find given integral...

Q: 0.8 0.6 0.4 0.2 of -0.2 -0.4 -0.6 0.5 1.5 2 5 A direction field for y'= -(2xy2 + y³) 2.5

A: Given differential equation is: y'=-2xy2+y3. We have to sketch the direction field for the given…

Q: [ u#(u – 1)"-1 đu (1+x!/n dx = n

Q: val (0

A: Introduction: The formula of the line integral ∫CF.dr, where C is the curve r(t) is given by,…

Q: 5. If X any Y are sets, then X-Y= {r€ X: 1¢Y} If X is open set and Y is closed set. Prove that (a)…

Q: a) Plot a direction field and some integral curves for xy'-2y=-1 on the rectangular region {-1<or…

A: a) given differential equation xy'-2y=-1 claim- plot a direction field and sole integral curves for…

Q: Find the quadratic approximation at (0,0) for f(x,y) = ln(1+x^2 + y^2).

Q: estigate whether the function u(x, y, z) = e^(3x+4y)cos(5z) is a harmonic function, where harmonic…

A: ux,y,z=e3x+4ycos5z

Q: Harry fills up his Jeep with gasoline and notes that the odometer reading is 23,511.9 miles. The…

Q: Q2-A) Find only the limits of integration of the following: YA yA R. ty=2 ア= z dydz ( cos e sin 8)…

Q: Determine which of the differentials (or both) is the total differential: a) 2[cos(2x +2y²) + x ] dx…

Q: Differentiate f(r) = 6x-2 cos z. Answer: f'(z) =

Q: integral of:

Question

x=J_y=K_z=L
Suppose G(J, K,L)= < 2 cos L, 6KL + eK,3K² – 2J sin L >
Then show: Gis conservative; find a potential function for G.
By the Fundamental Theorem for Line Integrals: Then, evaluate
SdP such that A is path defined by P (r) = < −5r + 4, 2rer−1,
COS
A
πr
> for r = [0,1]

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

SEE SOLUTION Check out a sample Q&A here

Step 1

Step 2

Step 3

Step 4

Step 5

Step by step

Solved in 5 steps

SEE SOLUTION Check out a sample Q&A here

Follow-up Questions

Read through expert solutions to related follow-up questions below.

Follow-up Question

Please show integration process. Is this the correct combination?

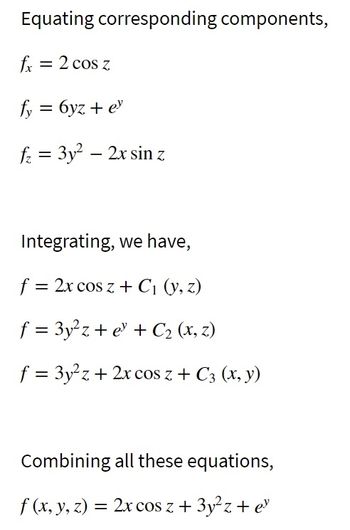
Equating corresponding components,
fx = 2 cos z
fy = 6yz + ey
f₂ = 3y² - 2x sin z
Integrating, we have,
f = 2x cos z + C₁ (y, z)
f = 3y²z+ e + C₂ (x, z)
f = 3y²z+ 2x cos z + C3 (x, y)
Combining all these equations,
f (x, y, z) = 2x cos z + 3y²z + ey

Solution

by Bartleby Expert

SEE SOLUTION

Similar questions

Ex: Find the F. T. of the rectangular pulse (gate function). f(t) = A rect ( ² ) = ATT (t/), I is the duration of the pulse. Sol: F(W) = 3 Tlz √ (A) coswt dt = 2A T1₂ sin (W) sinwt] = 2^ sin WI = A= W 2 Note that sincx- Sinx WZ → WI = I NIT W=2 n X n=1₂ 2₁ 3₁ Hello expert, I want you to explain how he got the value inside the circle Can you explain step by step and in a clear line, please? F(W) = AZ sinc (WI) Recall that Sincx = at x = + nT
Evaluate the integral S dy tan ¹(y/3)) (9+ y²) dy (tan¯1¹(y/3)) (9+y²) -
Q5) a) Use potential function to evaluate the following. e* Sin(y) dx + e*Cos(y)dy G.0)
Determine whether F = (e**y sin y, xe*ny cos y) is conservative and find a potential function if rsiny it is. Then evaluate F-dr, where C is the path (cos t,tcos 2t) from t = to t =-. 4
Give the general antiderivative for the integrand in the definite integral (cos x+ 1) dx Зл cos x+ 1 )dx.
Handwritten only
find Zet for : 2(x, y, t) = (os/2+4t) =< Sin(29) + Sin (64)
Find D (r,y, z) where f(x, y, z) = r'cos(y')cos(z') In the direction of v - (-9,16, 13). wwww of Possible Answers: 67.47 cos(y")cos(2²) – 44.98z*ycos(z²)sin(y²) – 44.98z" zcos(y²) sin(2) OA. O B. – 272°cos(y*)cos(z²) – 32r*ycos(z²)sin(y²) – 26" zcos(y²) sin(2) OC. 269.88z yzsin(y')sin(z²) O D. -1.2z cos(y')cos(z²) – 1.42a" ycos(z²)sin(y²) – 1.16z" zcos(v*) sin(z²) page Next page РОСОРНONE SHOT ON POCOPHONE F1
Let f(x, y, z) = x³ arctan z. Then solution.] af Əzəy (2,3,1)= aln 2 where a = . [Show
Given F(x,y) = < 3x^2e^y, x^3e^y + 1/y > is conservitive, Find the potential function phi(x,y) for F
Show that the differential form in the integral below is exact. Then evaluate the integral. (3,4,1) (0,0,0) ар ду 10x dx + 2y dy + 18z dz Compute the partial derivative.