-x² wave function y(x) = € 3², (−∞0 ≤ x ≤ +∞). If the wave function is not normalized, please determine the normalization constant. Standard Integrals: A. π¹/4 B. 1/¹/4 C. 1/(2¹/4) D. 1/(4 ¹/4) +∞ ·∞0 -ax² e 2 dx = 2πT α +∞ [te-o -∞ e-ax² dx = T α
-x² wave function y(x) = € 3², (−∞0 ≤ x ≤ +∞). If the wave function is not normalized, please determine the normalization constant. Standard Integrals: A. π¹/4 B. 1/¹/4 C. 1/(2¹/4) D. 1/(4 ¹/4) +∞ ·∞0 -ax² e 2 dx = 2πT α +∞ [te-o -∞ e-ax² dx = T α
Related questions
Question
![**Transcription for Educational Website:**
---
**Problem Statement:**
Consider the wave function \( \Psi(x) = e^{-\frac{x^2}{32}}, \, (-\infty \leq x \leq +\infty) \). If the wave function is not normalized, please determine the normalization constant.
**Standard Integrals:**
\[
\int_{-\infty}^{+\infty} e^{-\frac{ax^2}{2}} \, dx = \sqrt{\frac{2\pi}{a}}
\]
\[
\int_{-\infty}^{+\infty} e^{-ax^2} \, dx = \sqrt{\frac{\pi}{a}}
\]
**Options:**
A. \( \pi^{1/4} \)
B. \( 1/\pi^{1/4} \)
C. \( 1/(2 \pi^{1/4}) \)
D. \( 1/(4 \pi^{1/4}) \)
---
**Explanation of Diagrams (if applicable):**
There are no graphs or diagrams present in the image. The provided content consists of mathematical formulas and options related to the normalization of a given wave function in quantum mechanics. The integrals and options are standard forms and potential results for the normalization constant calculation.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fd6957468-6fb1-4659-9083-987b06676d6d%2F348af719-d519-4728-ba00-87f947201818%2Fx7lis9h_processed.png&w=3840&q=75)
Transcribed Image Text:**Transcription for Educational Website:**
---
**Problem Statement:**
Consider the wave function \( \Psi(x) = e^{-\frac{x^2}{32}}, \, (-\infty \leq x \leq +\infty) \). If the wave function is not normalized, please determine the normalization constant.
**Standard Integrals:**
\[
\int_{-\infty}^{+\infty} e^{-\frac{ax^2}{2}} \, dx = \sqrt{\frac{2\pi}{a}}
\]
\[
\int_{-\infty}^{+\infty} e^{-ax^2} \, dx = \sqrt{\frac{\pi}{a}}
\]
**Options:**
A. \( \pi^{1/4} \)
B. \( 1/\pi^{1/4} \)
C. \( 1/(2 \pi^{1/4}) \)
D. \( 1/(4 \pi^{1/4}) \)
---
**Explanation of Diagrams (if applicable):**
There are no graphs or diagrams present in the image. The provided content consists of mathematical formulas and options related to the normalization of a given wave function in quantum mechanics. The integrals and options are standard forms and potential results for the normalization constant calculation.
Expert Solution
Step 1: Given data
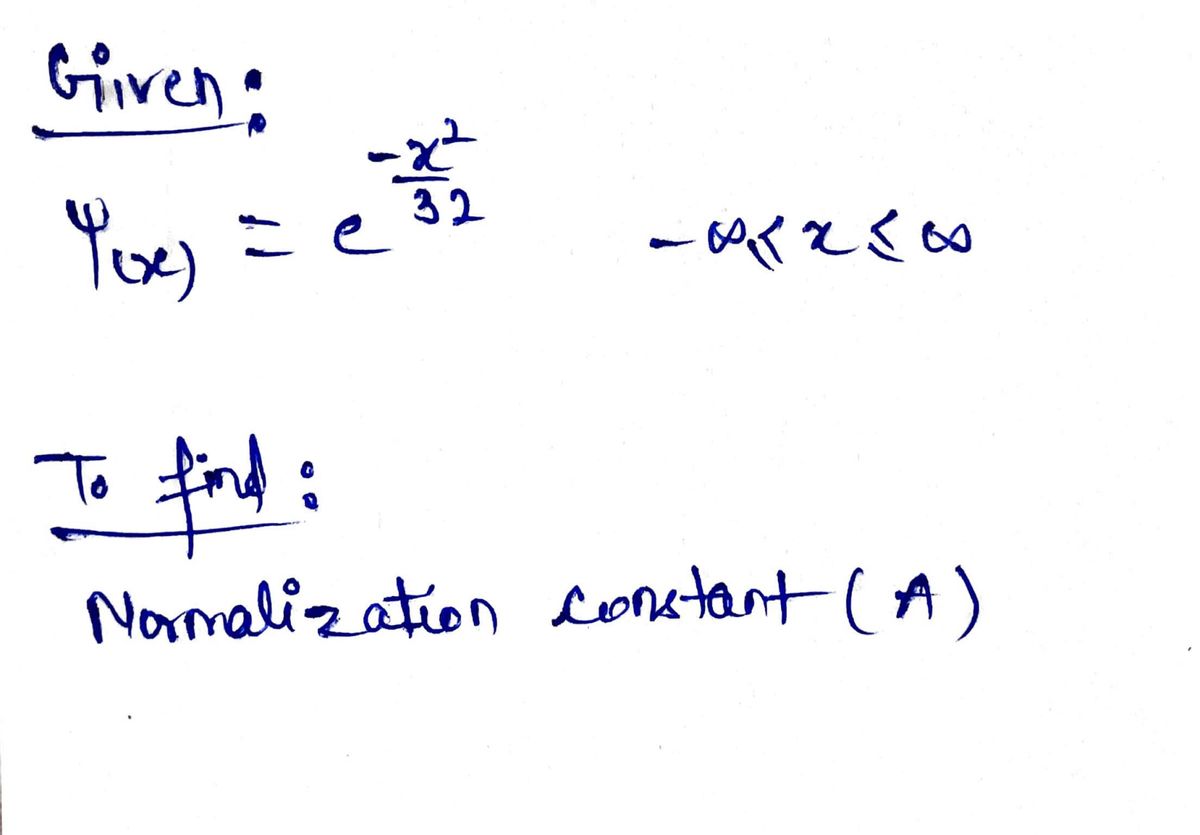
Step by step
Solved in 3 steps with 3 images
