wo particles, each of mass 3.21 x 10-4 kg and speed 6.81 m/s, travel in opposite directions along parallel lines separated by 5.49 cm. a) What is the magnitude L of the angular momentum of the two-particle system around a point midway between the two lines? (b) s the value different for a different location of the point? If the direction of either particle is reversed, what are the answers for (c) art (a) and (d) part (b)? (a) Number 0.000120 Units kg-m^2/s (b) yes (c) Number Units kg-m^2/s (d) yes

“Since you have posted a question with multiple sub-parts, we will solve first three sub-parts for you. To get remaining sub-part solved please repost the complete question and mention the sub-parts to be solved.”.
Given two particle have equal mass m=3.21x10-4kg
Moving with same speed v=6.81m/s
Line separate by d=5.49cm=0.0549m
Angular momentum is given by
.gif) ..................(1)
..................(1)
a)
When the two particles moves in opposite directions about middle point between them.

Here r+r=2r=d=0.0549m
Therefore angular momentum is
as we can see from equation (1) angular momentum due to both particle directed in the same direction. And 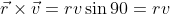
Therefore

This is the answer.
b) if centre of rotation is shifted then
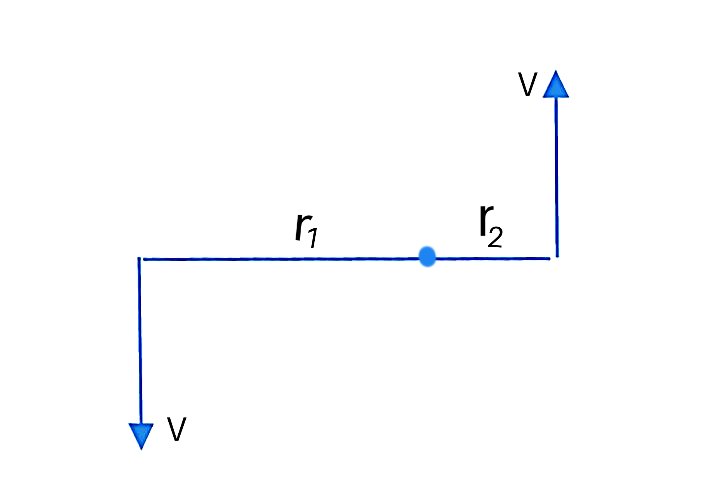
With r1+r2=d=0.0549m
Nowwe can see the direction of angular momentum due to each particle still remains same. Therefore value of angular momentum is
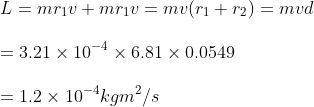
Therefore magnitude of angular momentum remains same.
Step by step
Solved in 5 steps with 8 images
