where Dx = X₁-X₂ and Dy = |Y₁ — Y2]. Assume that the two locations are independent and uniformly distributed over the square. a. Show that the joint pdf for D, and D, is (4(1-x)(1 − y), 0, fDxD, (x, y) = {4(1 − x) b. Define Ryx = D/Dx. Show that the pdf of Ryx is 2 fryx (r) = 1 33 1 3r3' 2 3r² 0≤x≤ 1,0≤ y ≤ 1 otherwise 0 ≤r≤1 1≤r≤00
where Dx = X₁-X₂ and Dy = |Y₁ — Y2]. Assume that the two locations are independent and uniformly distributed over the square. a. Show that the joint pdf for D, and D, is (4(1-x)(1 − y), 0, fDxD, (x, y) = {4(1 − x) b. Define Ryx = D/Dx. Show that the pdf of Ryx is 2 fryx (r) = 1 33 1 3r3' 2 3r² 0≤x≤ 1,0≤ y ≤ 1 otherwise 0 ≤r≤1 1≤r≤00
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter3: Functions And Graphs
Section3.3: Lines
Problem 20E
Related questions
Question

Transcribed Image Text:4. Consider a square service region of unit area in which travel is right angle and directions of travel are parallel
to the sides of the square. Let (X, Y₁) be the location of a mobile unit and (X₂, Y₂) the location of a demand
for service. The travel distance is
D =Dx + Dy
where
Dx = |X₁ - X₂ and Dy = |Y₁ — Y2\.
Assume that the two locations are independent and uniformly distributed over the square.
a. Show that the joint pdf for Dx and Dy is
(4(1-x)(1-y),
fpx.D¸y (x, y) = {4(1 –
b. Define Ryx = D/Dr. Show that the pdf of Ryx is
2
3
fryx (r) = .
2
3r²
1
r,
3
1
3r3'
0,
0≤x≤ 1,0 ≤ y ≤ 1
otherwise
0 ≤r≤1
1 ≤r <∞0
Expert Solution
Step 1: Distribution of product and ratio of two random variables obtained.


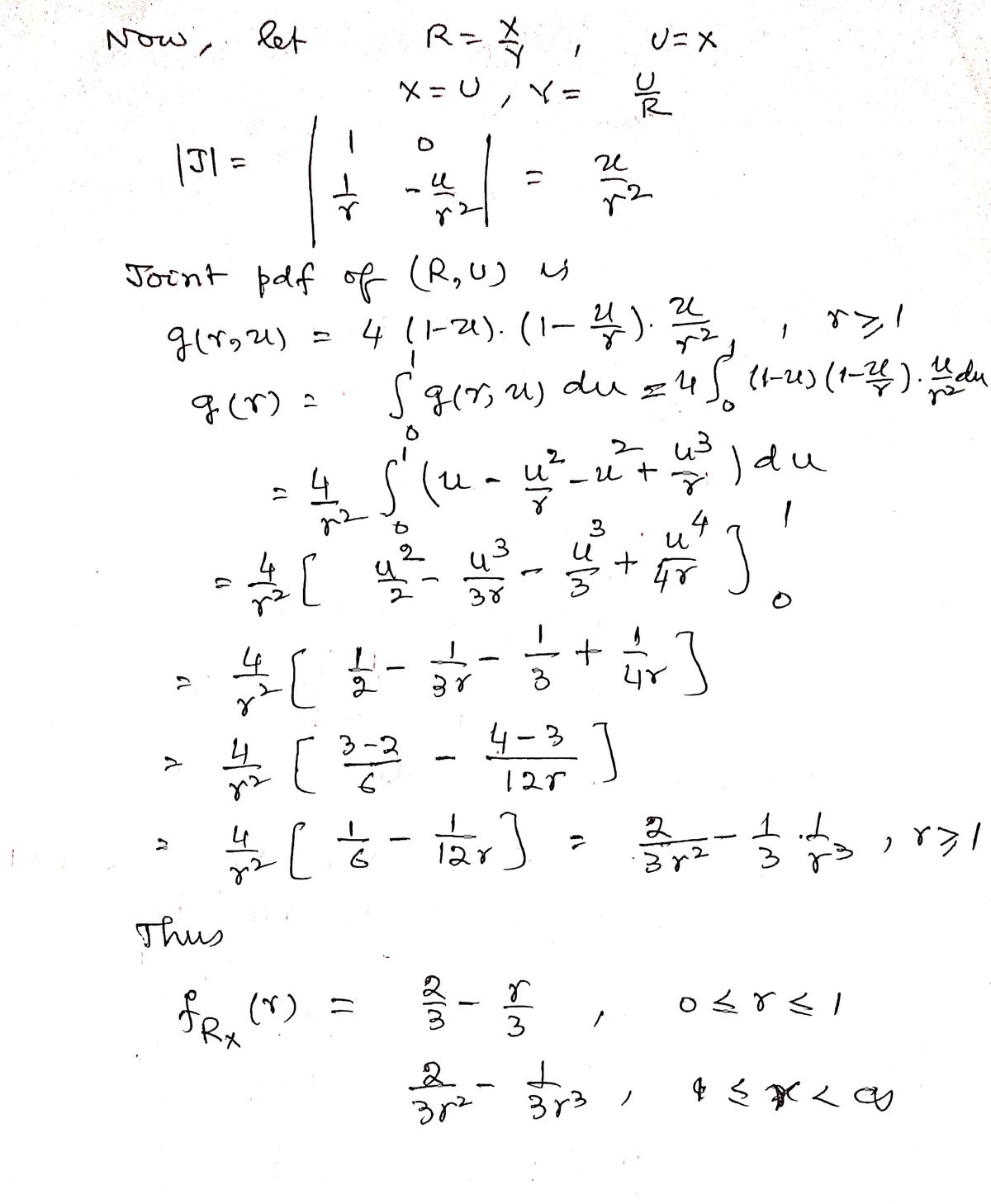
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning