What is the optimal time for a scuba diver to be on the bottom of the ocean? That depends on the depth of the dive. The U.S. Navy has done a lot of research on this topic. The Navy defines the "optimal time" to be the time at each depth for the best balance between length of work period and decompression time after surfacing. Let x = depth of dive in meters, and let y = optimal time in hours. A random sample of divers gave the following data. x 13.1 26.3 29.2 38.3 51.3 20.5 22.7 y 2.68 2.28 1.68 1.03 0.75 2.38 2.20 (d) Find the predicted optimal time in hours for a dive depth of x = 33 meters. (Round your answer to two decimal places.) hr (e) Find an 80% confidence interval for y when x = 33 meters. (Round your answers to two decimal places.) lower limit hr upper limit hr (f) Use a 1% level of significance to test the claim that β < 0. (Round your answers to two decimal places.) t = critical t = (g) Find a 90% confidence interval for β and interpret its meaning. (Round your answers to three decimal places.) lower limit upper limit
What is the optimal time for a scuba diver to be on the bottom of the ocean? That depends on the depth of the dive. The U.S. Navy has done a lot of research on this topic. The Navy defines the "optimal time" to be the time at each depth for the best balance between length of work period and decompression time after surfacing. Let x = depth of dive in meters, and let y = optimal time in hours. A random sample of divers gave the following data.
| x | 13.1 | 26.3 | 29.2 | 38.3 | 51.3 | 20.5 | 22.7 |
| y | 2.68 | 2.28 | 1.68 | 1.03 | 0.75 | 2.38 | 2.20 |
(d) Find the predicted optimal time in hours for a dive depth of x = 33 meters. (Round your answer to two decimal places.)
hr
(e) Find an 80% confidence interval for y when x = 33 meters. (Round your answers to two decimal places.)
| lower limit | hr |
| upper limit | hr |
(f) Use a 1% level of significance to test the claim that β < 0. (Round your answers to two decimal places.)
| t | = |
| critical t | = |
(g) Find a 90% confidence interval for β and interpret its meaning. (Round your answers to three decimal places.)
| lower limit | |
| upper limit |
Since you have posted a question with multiple sub-parts, we will solve first three sub-
parts for you. To get remaining sub-part solved please repost the complete question and
mention the sub-parts to be solved
Obtain predicted optimal time in hours for a dive depth of x =33meters.
Use EXCEL to obtain the regression equation.
EXCEL procedure:
- Go to EXCEL
- Go to Data>Data Analysis.
- Choose Regression.
- Input Y range as $B$1:$B$8.
- Input X range as $A$1:$A$8.
- Check the option Labels in First row.
- Click OK.
EXCEL output:
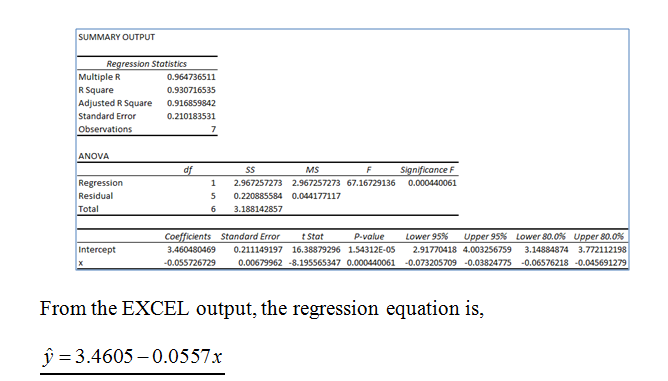
Substitute the value of x =33 in the regression equation.

The predicted optimal time in hours for a dive depth of x =33 meters is 1.62 hours.
Obtain the 80% confidence interval for y when x = 33 meters.
The 80% confidence interval for y when x = 33 meters is obtained below as follows:
The formula for the confidence interval is,

Use EXCEL Procedure for finding the critical value of t.
Follow the instruction to obtain the critical value of t:
- Open EXCEL
- Go to Formula bar.
- In formula bar enter the function as“=TINV”
- Enter the probability as 0.20.
- Enter the degrees of freedom as 5.
- Click enter.
EXCEL output:
From the EXCEL output, the critical value of t at the 0.20 level of significance with the 5 degrees of freedom is 1.4759.
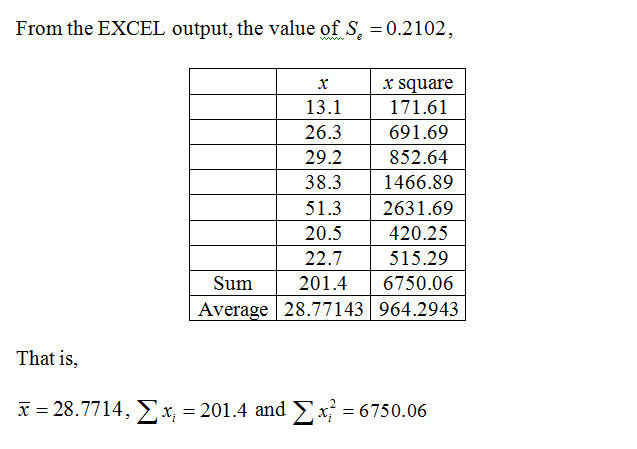
The required confidence interval is,

Thus, the lower limit for the 80% confidence interval when x=33 is 1.50 hr
The upper limit for the 80% confidence interval when x=33 is 1.75 hr.
Step by step
Solved in 3 steps with 7 images









