What are newtons laws of motion and intertial eference frames
Newton's first law of motion: it states that a body will not change its state of motion unless and until there is an unbalanced force act on it.it called /due to the inertia of a massive body . Or a body in rest will tend to be at rest and the body in motion with a constant velocity tend to remain in motion .
Newton's first law of motion essentially states that a point object subject to zero net external force moves in a straight-line with a constant speed (i.e., it does not accelerate). However, this is only true in special frames of reference called inertial frames. Indeed, we can think of Newton's first law as the definition of an inertial frame: i.e., an inertial frame of reference is one in which a point object subject to zero net external force moves in a straight-line with constant speed.
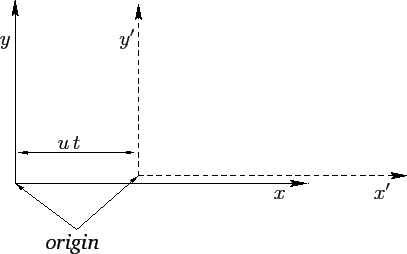
Suppose that we have found an inertial frame of reference. Let us set up a Cartesian coordinate system in this frame. The motion of a point object can now be specified by giving its position vector, 
, with respect to the origin of the coordinate system, as a function of time, 
. Consider a second frame of reference moving with some constant velocity 
with respect to the first frame. Without loss of generality, we can suppose that the Cartesian axes in the second frame are parallel to the corresponding axes in the first frame, that 
, and, finally, that the origins of the two frames instantaneously coincide at 
--see Figure 1. Suppose that the position vector of our point object is 
in the second frame of reference. It is evident, from Figure 1, that at any given time, , the coordinates of the object in the two reference frames satisfy
This coordinate transformation was first discovered by Galileo Galilei, and is known as a Galilean transformation in his honor.
By definition, the instantaneous velocity of the object in our first reference frame is given by 
, with an analogous expression for the velocity, 
, in the second frame. It follows from differentiation of Equations (1)-(3) with respect to time that the velocity components in the two frames satisfy
These equations can be written more succinctly v'=v-u
if an object is moving in a straight-line with constant speed in our original inertial frame (i.e., if 
) then it also moves in a (different) straight-line with (a different) constant speed in the second frame of reference (i.e., 
). Hence, we conclude that the second frame of reference is also an inertial frame.
A simple extension of the above argument allows us to conclude that there are an infinite number of different inertial frames moving with constant velocities with respect to one another
Step by step
Solved in 2 steps with 30 images
