Using the Law of Sines to solve the triangle if ZA = 40°, ZC = 69°, b = 13: ZB is degrees; a = C = Round to two decimal places if needed. Assume ZA is opposite side a, LB is opposite side b, and ZC is opposite side c.
Using the Law of Sines to solve the triangle if ZA = 40°, ZC = 69°, b = 13: ZB is degrees; a = C = Round to two decimal places if needed. Assume ZA is opposite side a, LB is opposite side b, and ZC is opposite side c.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
I need help.

Transcribed Image Text:**Using the Law of Sines to solve the triangle:**
Given:
- ∠A = 40°
- ∠C = 69°
- b = 13
**To Find:**
- ∠B
- Side a
- Side c
**Instructions:**
1. Calculate ∠B in degrees.
2. Determine the length of side a.
3. Determine the length of side c.
**Notes:**
- Round to two decimal places if needed.
- Assume ∠A is opposite side a, ∠B is opposite side b, and ∠C is opposite side c.
**Solution Steps:**
1. **Calculate ∠B:**
- Use the triangle angle sum property: ∠A + ∠B + ∠C = 180°.
- ∠B = 180° - 40° - 69°.
2. **Apply the Law of Sines:**
- The Law of Sines formula: (a/sinA) = (b/sinB) = (c/sinC).
- Use the known values to solve for the unknown sides.
Fill in the solutions for ∠B, a, and c in the provided spaces.
Expert Solution
Step 1
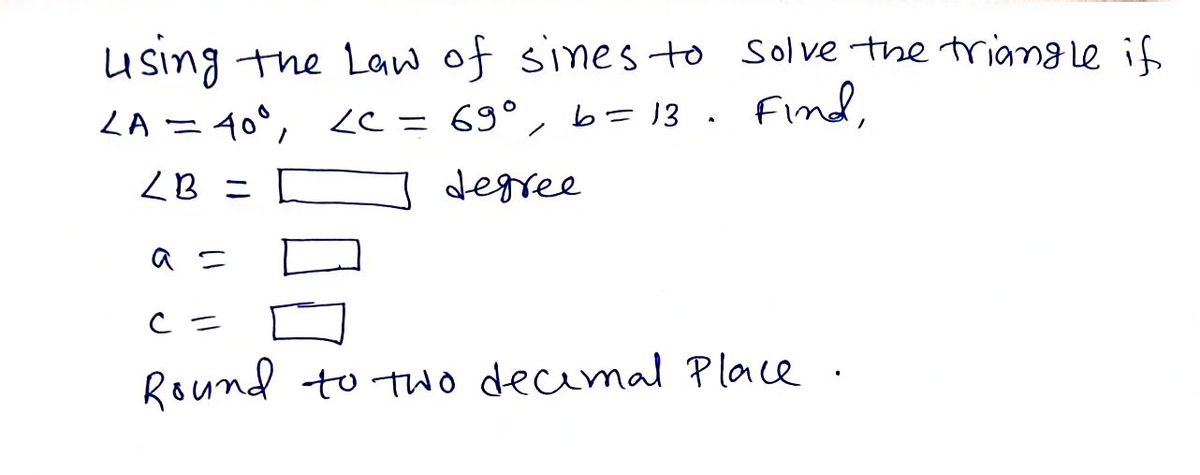
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

