What do I have to do ? Quadrilateral CART is dilated with the center at the origin and a scale factor of 6.**Task:**Describe Quadrilateral CART and Quadrilateral C'A'R'T' by completing the table below with the most appropriate answer.| Quadrilateral CART | Quadrilateral C'A'R'T' ||---------------------|------------------------|| (x, y) | ( , ) || C(-5, 15) | C'( , ) || A( , ) | A'(12, 6) || R( , ) | R'(-24, -12) || T(-25, 0) | T'( , ) |**Consider the following standard:**Given a figure in the coordinate plane and a scale factor, the coordinates of the new figure can be determined by multiplying the x and y coordinates of each point by the scale factor.

Name: What do I have to do ? Quadrilateral CART is dilated with the center a
Uploaded: 2024-03-05T11:52:21.000Z
Channel: Bartleby
Description: What do I have to do ? Quadrilateral CART is dilated with the center at the origin and a scale factor of 6.**Task:**Describe Quadrilateral CART and Quadrilateral C'A'R'T' by completing the table below with the most appropriate answer.| Quadrilateral

Answered: Quadrilateral CART is dilated with the…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Concept explainers

Topic Video

Question

What do I have to do ?

Quadrilateral CART is dilated with the center at the origin and a scale factor of 6.

**Task:**
Describe Quadrilateral CART and Quadrilateral C'A'R'T' by completing the table below with the most appropriate answer.

| Quadrilateral CART | Quadrilateral C'A'R'T' |
|---------------------|------------------------|
| (x, y) | ( , ) |
| C(-5, 15) | C'( , ) |
| A( , ) | A'(12, 6) |
| R( , ) | R'(-24, -12) |
| T(-25, 0) | T'( , ) |

**Consider the following standard:**

Given a figure in the coordinate plane and a scale factor, the coordinates of the new figure can be determined by multiplying the x and y coordinates of each point by the scale factor.

Expert Solution

Step 1

Step:-1

In given problem, dilation is used so first we need to understand about dilation and then using this definition, we'll solve the problem.

Dilation:- A dilation is a Transformation that produces an image that is the same shape as the original but the new image will be different in size from original. In this transformation, a scale factor is used.

For example:- Let the vertices of any shape is (a,b), (c, d), (E, F) and the center is origin then shape is dilated with scale factor k.

To dilate this shape, we multiply in the vertices of shape by scale factor k. So, the new vertices of the new shape is

$(k a, k b), (k c, k d), (k E, k F)$ .

Due to this scale factor the size of image either it will increase or decrease. It will depend on scale factor.

If 0 < k <1, then size of shape will decrease.

If k >1 then size of shape will increase.

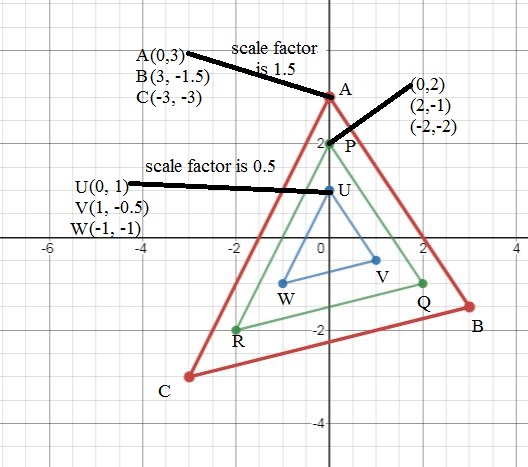
In this figure, PQR is original triangle and ABC and UVW are the dilated triangle of triangle PQR with scale factor 1.5 and 0.5 respectively.

Step 2

Step:-2

Now, given quadrilateral CART with center at origin and scale factor is $\frac{6}{5}$ .

if vertices of quadrilateral CART is (x,y) then new vertices of new quadrilateral C'A'R'T' is $(\frac{6}{5} x, \frac{6}{5} y)$

If C (-5, 15) then C' is $(\frac{6}{5} \times (- 5), \frac{6}{5} \times (15)) = (- 6, 18)$

Let A (a,b ) then A' is $(\frac{6}{5} a, \frac{6}{5} b)$ but given that A' = (12, 6) as both are the values of vertex A' so, both will same. then

$(\frac{6}{5} a, \frac{6}{5} b)$ =(12, 6)

multiply on both side by $\frac{5}{6}$ . we get

$\frac{5}{6} \times (\frac{6}{5} a, \frac{6}{5} b) = \frac{5}{6} \times (12, 6) \Rightarrow (\frac{5}{6} \times \frac{6}{5} a, \frac{5}{6} \times \frac{6}{5} b) = (\frac{5}{6} \times 12, \frac{5}{6} \times 6) \Rightarrow (a, b) = (10, 5)$

So, vertices of A is (10, 5)

Step:-3

Similarly, for R

Let vertices of R is (c, d) then R' is $(\frac{6}{5} c, \frac{6}{5} d)$ but given that R' =(-24, -12). So,

$(\frac{6}{5} c, \frac{6}{5} d)$ =(-24, -12)

multiply on both side by $\frac{5}{6}$ . we get

$\frac{5}{6} \times (\frac{6}{5} c, \frac{6}{5} c) = \frac{5}{6} \times (- 24, - 12) \Rightarrow (\frac{5}{6} \times \frac{6}{5} c, \frac{5}{6} \times \frac{6}{5} d) = (\frac{5}{6} \times (- 24), \frac{5}{6} \times (- 12)) \Rightarrow (c, d) = (- 20, - 10)$

So, vertices of R is (-20, -10)

Step:-4

Given that T (-25, 0) then $T' (\frac{6}{5} \times (- 25), \frac{6}{5} \times 0) = T' (- 30, 0)$

Trending now

This is a popular solution!

Step by step

Solved in 3 steps with 1 images

Knowledge Booster

$Application of Algebra$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Similar questions