Using R, plot the half of the integral area from — 2.5 to µ = 3.2 under the curve of the Gaussian density function ƒ with parameters µ = 3.2 and ² = 3. The curve to be plotted is on interval ( – 2.5, 9). Attach your source code.
Using R, plot the half of the integral area from — 2.5 to µ = 3.2 under the curve of the Gaussian density function ƒ with parameters µ = 3.2 and ² = 3. The curve to be plotted is on interval ( – 2.5, 9). Attach your source code.
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
Please provide a source code that can be copied into R programming.
The second image provides an example of what the code made look like and the guidelines with it
![x<-seq(-4,8,0.01)
y<-dnorm(x,2,1.5)
plot(x,y,type = "1")
polygon(c(x[x>4],4),c(y[x>4],y[x = =-
== -4]), col= "honeydew2")](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fdb82eee3-c597-43b7-b98f-cffc18fbca72%2F3824da95-5692-4225-9ed9-2453387113a4%2Fyrpdrn_processed.png&w=3840&q=75)
Transcribed Image Text:x<-seq(-4,8,0.01)
y<-dnorm(x,2,1.5)
plot(x,y,type = "1")
polygon(c(x[x>4],4),c(y[x>4],y[x = =-
== -4]), col= "honeydew2")

Transcribed Image Text:Using R, plot the half of the integral area from - 2.5 to µ = 3.2 under the curve of the Gaussian
density function f with parameters µ = 3.2 and ² = 3. The curve to be plotted is on interval
( – 2.5, 9). Attach your source code.
Expert Solution
Step 1
Given using R code we have to plot the half of the integral area from -2.5 to 3.2 under the curve of the gaussian density function with parameters mean=3.2 and variance=3. We have to plot the curve on interval(-2.5,9).
Step by step
Solved in 3 steps with 1 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
This code is not being accepted. Please look at this image and explain what I am doing incorrect. Please put the code in 4 succesive lines so it can be copied all at once.
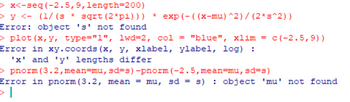
Transcribed Image Text:>x<-seg (-2.5,9, length=200)
> y < (1/(s* sqrt (2*pi))) *exp(-((x-mu) ^2)/(2*s^2))
Error: object 's' not found
> plot (x, y, type="1", 1wd=2, col = "blue", xlim = c(-2.5,9))
Error in xy.coords (x, y, xlabel, ylabel, log) :
'x' and 'y' lengths differ
>pnorm (3.2, mean-mu, sd-s) -pnorm (-2.5, mean-mu, sd=s)
Error in pnorm (3.2, mean = mu, sd = s) : object 'mu' not found
>I
Solution
Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman