) Using either Prim's or Kruskal's algorithms, determine the cost of the minimum spannin tree which will connect all the vertices of the graph below. State which algorithm you used. 5) Sketch the minimum spanning tree. 5 F 4 2 2 B 1 8 K 13 m 7 H 4 2 2 7 3 1 12 16 M
) Using either Prim's or Kruskal's algorithms, determine the cost of the minimum spannin tree which will connect all the vertices of the graph below. State which algorithm you used. 5) Sketch the minimum spanning tree. 5 F 4 2 2 B 1 8 K 13 m 7 H 4 2 2 7 3 1 12 16 M
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:### Task Description
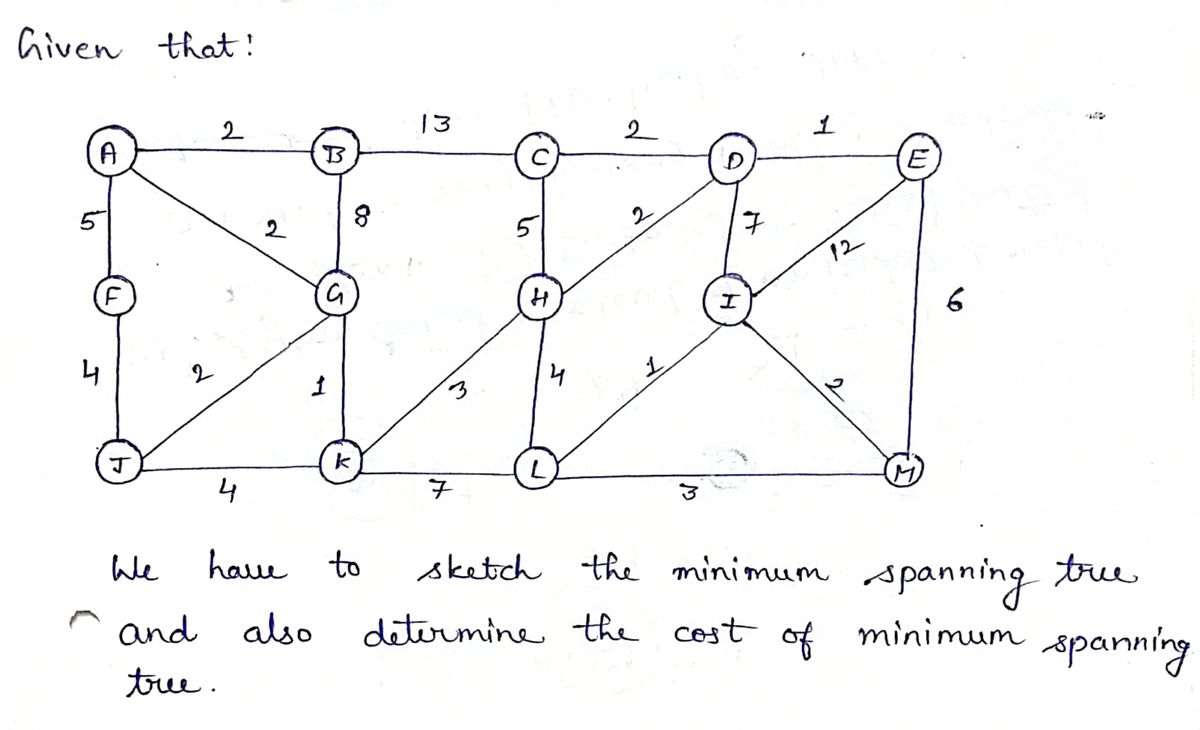
#### a)
Using either Prim’s or Kruskal’s algorithms, determine the cost of the minimum spanning tree which will connect all the vertices of the graph below. State which algorithm you used.
#### b)
Sketch the minimum spanning tree.
### Graph Details
The graph is composed of the following vertices and edges along with their respective weights:
- **Vertices:** A, B, C, D, E, F, G, H, I, J, K, L, M
- **Edges and Weights:**
- A - B : 2
- A - F : 5
- A - G : 2
- B - C : 13
- B - G : 8
- C - D : 2
- D - E : 1
- D - I : 7
- E - I : 12
- E - M : 6
- F - J : 4
- G - H : 5
- G - K : 1
- H - I : 2
- H - L : 4
- I - M : 2
- J - K : 4
- K - L : 7
- L - M : 3
### Exploring Algorithms: Prim's and Kruskal's
For effective problem-solving, you can focus on two popular algorithms for finding a minimum spanning tree (MST): **Prim’s Algorithm** and **Kruskal’s Algorithm**. Both aim to connect all vertices with the minimum total edge weight, but they differ in approach:
- **Prim’s Algorithm** starts from an arbitrary node and grows the MST by adding the smallest-weight edge from the existing tree to a vertex outside the tree.
- **Kruskal’s Algorithm** sorts all edges by weight and adds the smallest edge to the MST, ensuring no cycles are formed.
### Suggested Steps to Solve:
1. **Initialize** a starting point (for Prim’s) or sort edges (for Kruskal’s).
2. **Iterate** through the process, adding edges one by one to form the MST while avoiding cycles.
3. **Calculate the total weight** of the selected edges to determine the cost of the MST.
To achieve a comprehensive understanding, visualize the MST by sketching out the selected edges on the
Expert Solution
Step 1: Graph
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

