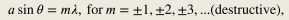Using coding Here you are asked to implement the method by dividing the aperture into a finite
Using coding Here you are asked to implement the method by dividing the aperture into a finite
number of segments. Use a unit system where lengths are measured as multiples of
the wavelength of the incident light, λ. Assume that the index of refraction n = 1.00
can be used for air.
Further assume that the horizontal distance between source and aperture X is some
large multiple of λ, and that the same distance is assumed between aperture and
detector screen.
Assume that the aperture size a is some small multiple of the wavelength.
a) Compute the probability amplitude for the central detector height yd = 0 by
using three paths (i) one going directly from source (at height ys = 0, i.e., on the x
axis, via yi = 0 (at the aperture) towards the detector screen;
(ii) then for two straight-line paths: one going via yi = a/2, and one vie yi = −a/2.
The result should be three complex numbers. Show that these are unit-magnitude
complex numbers.
b) Calculate the relative probability for arrival at the detector height y = 0 by
adding the three amplitudes and forming the magnitude squared.
Step by step
Solved in 5 steps with 3 images

adding on to the question:
Now choose the detector height (on one side, i.e., y > 0 or y < 0) that
corresponds to an angle where the first minimum in the intensity pattern is expected.
formula given in the picture below m = 1. Repeat the
computations with three paths as before (passing through yi = 0, and yi = ±a/2),
and obtain the relative arrival probability. What is the intensity ratio compared to
the central detector location yd = 0?