Use Table A to find the value z of a standard Normal variable that satisfies each of the following conditions. Use the value of z from Table A that comes closest to satisfying the condition. In each case, sketch a standard Normal curve with your value of z marked on the axis. (a) Find the point z with 66% of the observations falling below it. Enter your answer rounded to two decimal places. z= (b) Find the point z with 24% of the observations falling above it. Enter your answer rounded to two decimal places. z=
Use Table A to find the value z of a standard Normal variable that satisfies each of the following conditions. Use the value of z from Table A that comes closest to satisfying the condition. In each case, sketch a standard Normal curve with your value of z marked on the axis. (a) Find the point z with 66% of the observations falling below it. Enter your answer rounded to two decimal places. z= (b) Find the point z with 24% of the observations falling above it. Enter your answer rounded to two decimal places. z=
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Concept explainers
Continuous Probability Distributions
Probability distributions are of two types, which are continuous probability distributions and discrete probability distributions. A continuous probability distribution contains an infinite number of values. For example, if time is infinite: you could count from 0 to a trillion seconds, billion seconds, so on indefinitely. A discrete probability distribution consists of only a countable set of possible values.
Normal Distribution
Suppose we had to design a bathroom weighing scale, how would we decide what should be the range of the weighing machine? Would we take the highest recorded human weight in history and use that as the upper limit for our weighing scale? This may not be a great idea as the sensitivity of the scale would get reduced if the range is too large. At the same time, if we keep the upper limit too low, it may not be usable for a large percentage of the population!
Question
Use Table A to find the value z of a standard Normal variable that satisfies each of the following conditions. Use the value of z from Table A that comes closest to satisfying the condition. In each case, sketch a standard Normal curve with your value of z marked on the axis.
(a) Find the point z with 66% of the observations falling below it. Enter your answer rounded to two decimal places.
z=
(b) Find the point z with 24% of the observations falling above it. Enter your answer rounded to two decimal places.
z=
Transcribed Image Text:696
TABLES
Table entry for z is the area under the
Table entry
standard Normal curve to the left of z.
TABLE A Standard normal cumulative proportions
.00
.01
.02
.03
.04
.05
.06
.07
.08
.09
-3.4
.0003
.0003
.0003
.0003
.0003
.0003
.0003
.0003
.0003
.0002
.0003
.0005
.0007
.0005
.0004
.0006
-3.3
.0005
.0005
.0004
.0004
.0004
.0004
.0004
-3.2
.0007
.0007
.0006
.0006
.0006
.0006
.0005
.0005
-3.1
.0010
.0009
.0009
.0009
.0008
.0008
.0008
.0008
.0007
-3.0
.0013
.0013
.0013
.0012
.0012
.0011
.0011
.0011
.0010
.0010
-2.9
.0019
.0018
.0018
.0017
.0016
.0016
.0015
.0015
.0014
.0014
.0023
.0032
-2.8
.0026
.0025
.0024
.0023
.0022
.0021
.0021
.0020
.0019
-2.7
.0035
.0034
.0033
.0031
.0030
.0029
.0028
.0027
.0026
-2.6
.0047
.0045
.0044
.0043
.0041
.0040
.0054
.0039
.0038
.0037
.0036
-2.5
.0062
.0060
.0059
.0057
.0055
.0052
.0051
.0049
.0048
-2.4
.0064
.0084
.0082
.0080
.0078
.0075
.0073
.0071
.0069
.0068
.0066
-2.3
.0107
.0104
.0102
.0099
.0096
.0094
.0091
.0089
.0087
-2.2
.0139
.0136
.0132
.0129
.0125
.0122
.0119
.0116
.0113
.0110
.0174
.0222
.0170
.0217
-2.1
.0179
.0166
.0162
.0158
.0154
.0150
.0146
.0143
-2.0
.0228
.0212
.0207
.0202
.0197
.0192
.0188
.0183
.0274
.0287
.0359
.0281
.0268
.0262
.0256
.0250
.0233
.0244
.0307
.0384
-1.9
.0239
.0314
- 1.8
- 1.7
.0336
.0418
.0516
.0329
.0409
.0351
.0344
.0322
.0301
.0294
.0446
.0436
.0427
.0401
.0392
.0375
.0367
.0485
.0505
.0618
.0455
.0548
.0668
-1.6
.0537
.0526
.0495
.0475
.0465
-1.5
.0655
.0643
.0630
.0606
.0594
.0582
.0571
.0559
-1.4
-1.3
.0694
.0838
.0808
.0793
.0778
.0764
.0749
.0735
.0721
.0708
.0681
.0968
.0951
.0934
.0918
.0901
.0885
.0869
.0853
.0823
- 1.2
- 1.1
.1038
.1230
.1151
.1131
.1112
.1093
.1075
.1056
.1020
.1003
.0985
.1357
.1335
.1314
.1292
.1271
.1251
.1210
.1190
.1170
-1.0
.1587
.1562
.1539
.1515
.1492
.1469
.1446
.1423
.1401
.1379
.1814
.2090
-0.9
.1841
.1788
.1762
.1736
.1711
.1685
.1660
.1635
.1611
-0.8
.2119
.2061
.2033
.2005
.1977
.1949
.1922
.1894
.1867
-0.7
.2420
.2389
.2358
.2327
.2296
.2266
.2236
.2206
.2177
.2148
-0.6
.2743
.2709
.2676
.2643
.2611
.2578
.2546
.2514
.2483
.2451
-0.5
3085
3050
.3015
.2981
.2946
.2912
.2877
.2843
.2810
.2776
.3409
.3783
.4168
-0.4
.3446
.3372
.3336
3300
.3264
.3228
.3192
.3156
.3121
-0.3
.3821
.3745
3707
.3669
.3632
.3594
.3557
3520
.3483
.4090
.4483
.4880
-0.2
.4207
.4129
.4052
.4013
.3974
.3936
.3897
.3859
.4404
.4801
.4247
.4641
-0.1
.4602
.4562
.4522
.4443
.4364
.4325
.4286
-0.0
.5000
.4960
.4920
.4840
.4761
.4721
.4681
Transcribed Image Text:TABLES
697
Table entry
Table entry for z is the area under the
standard Normal curve to the left of z.
TABLE A Standard Normal cumulative proportions (continued)
.00
.01
.02
.03
.04
.05
.06
.07
.08
.09
0.0
.5000
.5040
.5080
.5120
.5160
.5199
.5239
.5279
.5319
.5359
.5557
.5948
.6331
.5636
.6026
0.1
.5398
.5438
.5478
.5517
.5596
.5675
.5714
.5753
0.2
.5793
.5832
.5871
.5910
.5987
.6064
.6103
.6141
0.3
0.4
.6406
.6772
.6480
.6844
.6179
.6217
.6255
.6293
.6368
.6443
.6517
.6554
.6591
.6628
.6664
.6700
.6736
.6808
.6879
.6950
.7054
.7389
.7088
.7422
.7123
.7454
.7764
0.5
.6915
.6985
.7019
.7157
.7190
.7224
0.6
.7257
.7580
.7517
.7823
.8106
.7291
.7324
.7357
.7486
.7794
.8078
.8340
.7549
0.7
.7611
.7642
.7673
.7704
.7734
.7852
.8023
.8289
0.8
.7881
.7910
.7939
.7967
.7995
.8051
.8133
0.9
.8159
.8186
.8212
.8238
.8264
.8315
.8365
.8389
.8485
.8708
.8907
.8508
.8577
.8790
1.0
.8413
.8438
.8461
.8531
.8554
.8599
.8621
.8643
.8849
.8749
.8944
1.1
.8665
.8686
.8729
.8770
.8810
.8830
1.2
.8869
.8888
.8925
.8962
.8980
.8997
.9015
1.3
.9032
.9049
.9066
.9082
.9099
.9115
.9131
.9147
.9162
.9177
1.4
.9192
.9207
.9222
.9236
.9251
.9265
.9279
.9292
.9306
.9319
1.5
.9332
.9345
.9357
.9370
.9382
.9394
.9406
.9418
.9429
.9441
.9463
.9564
1.6
.9452
.9474
.9484
.9495
.9505
.9515
.9525
.9535
.9545
1.7
.9554
.9573
.9582
.9591
.9599
.9608
.9616
.9625
.9633
.9678
.9744
1.8
.9641
.9649
.9656
.9664
.9671
.9686
.9693
.9699
.9706
1.9
.9713
.9719
.9726
.9732
.9738
.9750
.9756
.9761
.9767
2.0
.9772
.9778
.9783
.9788
.9793
.9798
.9803
.9808
.9812
.9817
2.1
.9821
.9826
.9830
.9834
.9838
.9842
.9846
.9850
.9854
.9887
.9913
.9857
2.2
.9861
.9864
.9868
.9871
.9875
.9878
.9881
.9884
.9890
2.3
.9893
.9896
.9898
.9901
.9904
.9906
.9909
.9911
.9916
2.4
.9918
.9920
.9922
.9925
.9927
.9929
.9931
.9932
.9934
.9936
2.5
.9938
.9940
.9941
.9943
.9945
.9946
.9948
.9949
.9951
.9952
2.6
.9953
.9955
.9956
.9957
.9959
.9960
.9961
.9962
.9963
.9964
2.7
.9965
.9966
.9967
.9968
.9969
.9970
.9971
.9972
.9973
.9974
.9977
.9983
2.8
.9974
.9975
.9976
.9977
.9978
.9979
.9979
.9980
.9981
2.9
.9981
.9982
.9982
.9984
.9984
.9985
.9985
9986
.9986
3.0
.9987
.9987
.9987
.9988
9988
.9989
.9989
.9989
.9990
.9990
3.1
.9990
.9991
.9991
.9991
.9992
.9992
.9992
.9992
.9993
.9993
3.2
.9993
.9993
.9994
.9994
.9994
.9994
.9994
.9996
.9995
.9995
.9995
3.3
.9995
.9995
.9995
.9996
.9996
.9996
.9996
.9996
.9997
3.4
.9997
.9997
.9997
.9997
.9997
.9997
.9997
.9997
.9997
.9998
Expert Solution
Step 1
a)
The point z with 66% of the observations falling below it is obtained as below:
The value of z is obtained as follows:
The value of z is obtained from Excel using "=NORMSINV(probability)".
Output obtained using Excel is given below:
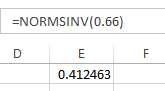
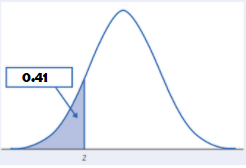
From the output, the z value is 0.41.
Thus, the point z with 66% of the observations falling below it is 0.41.
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 4 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Recommended textbooks for you
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON
The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman