Use proof by contradiction to show that 2 is not a rational number. Note that you may use the theorem stated in question 14.
Use proof by contradiction to show that 2 is not a rational number. Note that you may use the theorem stated in question 14.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Topic Video
Question
![**Proof by Contradiction: Showing that \(\sqrt{2}\) is Not a Rational Number**
To demonstrate that \(\sqrt{2}\) is not a rational number, we'll use a proof by contradiction. Assume that \(\sqrt{2}\) is rational, which means it can be expressed as a fraction \(\frac{a}{b}\) where \(a\) and \(b\) are integers with no common factors other than 1 (i.e., the fraction is in its simplest form) and \(b \neq 0\).
Start by expressing \(\sqrt{2}\) as:
\[
\sqrt{2} = \frac{a}{b}
\]
Squaring both sides, we have:
\[
2 = \frac{a^2}{b^2}
\]
This implies:
\[
a^2 = 2b^2
\]
From this equation, we can see that \(a^2\) is even because it equals \(2\) times an integer (\(b^2\)). Since \(a^2\) is even, \(a\) must also be even. Let \(a = 2k\) for some integer \(k\).
Substituting \(a = 2k\) into the equation \(a^2 = 2b^2\), we get:
\[
(2k)^2 = 2b^2
\]
\[
4k^2 = 2b^2
\]
\[
2k^2 = b^2
\]
This equation shows that \(b^2\) is even, which means \(b\) is also even.
Since both \(a\) and \(b\) are even, they have a common factor of \(2\). This contradicts our initial assumption that \(\frac{a}{b}\) was in its simplest form. Therefore, \(\sqrt{2}\) cannot be expressed as a fraction of two integers, proving that it is not a rational number.
*Note: You may use the theorem stated in question 14 to further justify this proof or explore related concepts.*](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F7107a648-c1c3-4f17-8c97-d0a63b112acb%2F93f61878-a74b-44a8-a3eb-8a83e3ce01eb%2Fwaijwak_processed.png&w=3840&q=75)
Transcribed Image Text:**Proof by Contradiction: Showing that \(\sqrt{2}\) is Not a Rational Number**
To demonstrate that \(\sqrt{2}\) is not a rational number, we'll use a proof by contradiction. Assume that \(\sqrt{2}\) is rational, which means it can be expressed as a fraction \(\frac{a}{b}\) where \(a\) and \(b\) are integers with no common factors other than 1 (i.e., the fraction is in its simplest form) and \(b \neq 0\).
Start by expressing \(\sqrt{2}\) as:
\[
\sqrt{2} = \frac{a}{b}
\]
Squaring both sides, we have:
\[
2 = \frac{a^2}{b^2}
\]
This implies:
\[
a^2 = 2b^2
\]
From this equation, we can see that \(a^2\) is even because it equals \(2\) times an integer (\(b^2\)). Since \(a^2\) is even, \(a\) must also be even. Let \(a = 2k\) for some integer \(k\).
Substituting \(a = 2k\) into the equation \(a^2 = 2b^2\), we get:
\[
(2k)^2 = 2b^2
\]
\[
4k^2 = 2b^2
\]
\[
2k^2 = b^2
\]
This equation shows that \(b^2\) is even, which means \(b\) is also even.
Since both \(a\) and \(b\) are even, they have a common factor of \(2\). This contradicts our initial assumption that \(\frac{a}{b}\) was in its simplest form. Therefore, \(\sqrt{2}\) cannot be expressed as a fraction of two integers, proving that it is not a rational number.
*Note: You may use the theorem stated in question 14 to further justify this proof or explore related concepts.*
Expert Solution
Step 1
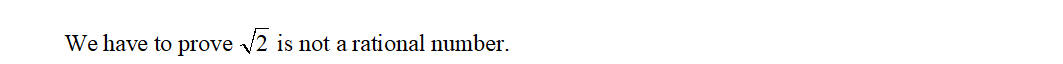
Step by step
Solved in 2 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

