Answered: Use a software program or a graphing…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Concept explainers

Question

Use a software program or a graphing utility to
(a) find the transition matrix from B to B′,
(b) find the transition matrix from B′ to B,
(c) verify that the two transition matrices are inverses of each other, and
(d) find the coordinate matrix [x]_B, given the coordinate matrix [x]_B′.
B = {(1, −1, 9), (−9, 1, 1), (1, 9, −1)},
B′ = {(3, 0, 3), (−3, 3, 0), (0, −3, 3)},
[x]_B′ = [−5 −4 1]^T

Expert Solution

Step 1: Find the transition matrix from B to B'.

(a)

The given bases are:

$table attributes columnalign right center left columnspacing 0px end attributes row B equals cell open curly brackets open parentheses 1 comma negative 1 comma 9 close parentheses comma open parentheses negative 9 comma 1 comma 1 close parentheses comma open parentheses 1 comma 9 comma negative 1 close parentheses close curly brackets end cell row cell B apostrophe end cell equals cell open curly brackets open parentheses 3 comma 0 comma 3 close parentheses comma open parentheses negative 3 comma 3 comma 0 close parentheses comma open parentheses 0 comma negative 3 comma 3 close parentheses close curly brackets end cell end table$

Now, write augmented matrix: $open square brackets B colon B apostrophe close square brackets equals open square brackets table row 1 cell negative 9 end cell 1 row cell negative 1 end cell 1 9 row 9 1 cell negative 1 end cell end table left enclose table row 3 cell negative 3 end cell 0 row 0 3 cell negative 3 end cell row 3 0 3 end table end enclose close square brackets$ .

The reduced row echelon form is as shown below.

So, the transition matrix from B to B' is:

$P equals box enclose open square brackets table row cell 0.373 end cell cell negative 0.008 end cell cell 0.3 end cell row cell negative 0.284 end cell cell 0.365 end cell 0 row cell 0.073 end cell cell 0.292 end cell cell negative 0.3 end cell end table close square brackets end enclose$ .

Step 2: Find the transition matrix from B' to B.

(b)

The given bases are:

Now, write augmented matrix: $open square brackets B apostrophe colon B close square brackets equals open square brackets table row 3 cell negative 3 end cell 0 row 0 3 cell negative 3 end cell row 3 0 3 end table left enclose table row 1 cell negative 9 end cell 1 row cell negative 1 end cell 1 9 row 9 1 cell negative 1 end cell end table end enclose close square brackets$ .

The reduced row echelon form is as shown below.

So, the transition matrix from B' to B is:

$Q equals box enclose open square brackets table row cell 1.5 end cell cell negative 1.17 end cell cell 1.5 end cell row cell 1.17 end cell cell 1.83 end cell cell 1.17 end cell row cell 1.5 end cell cell 1.5 end cell cell negative 1.83 end cell end table close square brackets end enclose$ .

Step 3: Verify that the matrices are inverse of each other.

(c)

Find the product $P Q$ .

$P Q equals open square brackets table row cell 0.373 end cell cell negative 0.008 end cell cell 0.3 end cell row cell negative 0.284 end cell cell 0.365 end cell 0 row cell 0.073 end cell cell 0.292 end cell cell negative 0.3 end cell end table close square brackets open square brackets table row cell 1.5 end cell cell negative 1.17 end cell cell 1.5 end cell row cell 1.17 end cell cell 1.83 end cell cell 1.17 end cell row cell 1.5 end cell cell 1.5 end cell cell negative 1.83 end cell end table close square brackets$ .

Using graphic calculator the prdocut is shown below.

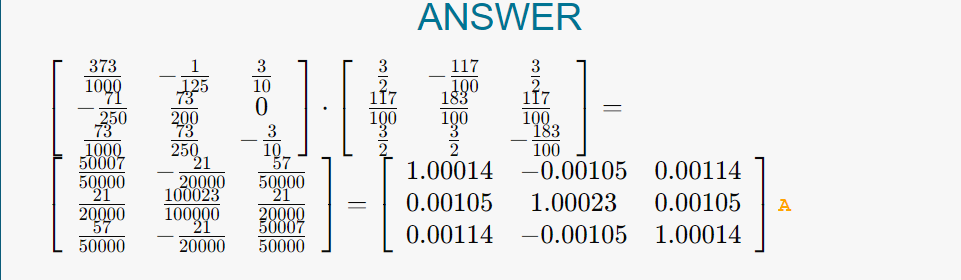
So, we can see that:

$P Q equals open square brackets table row 1 0 0 row 0 1 0 row 0 0 1 end table close square brackets$ .

So, both the matrices are inverse of each other.

Step by step

Solved in 5 steps with 20 images

Knowledge Booster

$Vector Space$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Similar questions