Two infinite, very thin and flat sheets of insulating material carry electric charge o > 0 per unit area. The charge density is homogeneous. Sheet 1 lays d. The electric fields generated by the sheets at y 0, and sheet 2 at y independently, that is, when the other sheet is absent, are E, = {3 {. - for y > d 2€0 i for y >0 (1) 2€0 E2 for y <0 ' 2€0 for y < d 2€0* 1. Make a sketch of the system of two sheets, including the coordinate system. 2. Use the principle of superposition, E = E1+E2, to compute the electric field vector E generated by the two sheets (a) for y < 0, (b) for 0 < y < d, (c) and for d < y. 3. Plot Eg, Ey, E, and |E| = /E + E; + E? as a function of y.
Two infinite, very thin and flat sheets of insulating material carry electric charge o > 0 per unit area. The charge density is homogeneous. Sheet 1 lays d. The electric fields generated by the sheets at y 0, and sheet 2 at y independently, that is, when the other sheet is absent, are E, = {3 {. - for y > d 2€0 i for y >0 (1) 2€0 E2 for y <0 ' 2€0 for y < d 2€0* 1. Make a sketch of the system of two sheets, including the coordinate system. 2. Use the principle of superposition, E = E1+E2, to compute the electric field vector E generated by the two sheets (a) for y < 0, (b) for 0 < y < d, (c) and for d < y. 3. Plot Eg, Ey, E, and |E| = /E + E; + E? as a function of y.
Related questions
Question
![### Two Infinite, Very Thin Flat Sheets of Insulating Material
Two infinite, very thin, and flat sheets of insulating material carry an electric charge \( \sigma > 0 \) per unit area. The charge density is homogeneous. Sheet 1 lies at \( y = 0 \), and sheet 2 at \( y = d \).
The electric fields generated by the sheets independently are:
\[
\mathbf{E_1} =
\begin{cases}
\frac{\sigma}{2\varepsilon_0} \hat{\mathbf{j}} & \text{for } y > 0 \\
-\frac{\sigma}{2\varepsilon_0} \hat{\mathbf{j}} & \text{for } y < 0
\end{cases}
\]
\[
\mathbf{E_2} =
\begin{cases}
\frac{\sigma}{2\varepsilon_0} \hat{\mathbf{j}} & \text{for } y > d \\
-\frac{\sigma}{2\varepsilon_0} \hat{\mathbf{j}} & \text{for } y < d
\end{cases}
\]
### Tasks
1. **Sketch the System**: Draw the system of two sheets, and include the coordinate system.
2. **Compute the Electric Field Vector using Superposition**:
- Use the principle of superposition, \( \mathbf{E} = \mathbf{E_1} + \mathbf{E_2} \), to find the electric field vector \( \mathbf{E} \) generated by the two sheets:
- (a) for \( y < 0 \)
- (b) for \( 0 < y < d \)
- (c) for \( d < y \)
3. **Plot Electric Field Components**: Plot \( E_x \), \( E_y \), \( E_z \) and \( |\mathbf{E}| = \sqrt{E_x^2 + E_y^2 + E_z^2} \) as a function of \( y \).
This exercise explores the properties of electric fields in the presence of charged flat sheets and applies the superposition principle to calculate the net field.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F289f06d3-ff79-44a0-9e06-63a38c7e8148%2F20a55958-4e62-4b4f-8822-ed805a3d731f%2Fru7vv5f_processed.png&w=3840&q=75)
Transcribed Image Text:### Two Infinite, Very Thin Flat Sheets of Insulating Material
Two infinite, very thin, and flat sheets of insulating material carry an electric charge \( \sigma > 0 \) per unit area. The charge density is homogeneous. Sheet 1 lies at \( y = 0 \), and sheet 2 at \( y = d \).
The electric fields generated by the sheets independently are:
\[
\mathbf{E_1} =
\begin{cases}
\frac{\sigma}{2\varepsilon_0} \hat{\mathbf{j}} & \text{for } y > 0 \\
-\frac{\sigma}{2\varepsilon_0} \hat{\mathbf{j}} & \text{for } y < 0
\end{cases}
\]
\[
\mathbf{E_2} =
\begin{cases}
\frac{\sigma}{2\varepsilon_0} \hat{\mathbf{j}} & \text{for } y > d \\
-\frac{\sigma}{2\varepsilon_0} \hat{\mathbf{j}} & \text{for } y < d
\end{cases}
\]
### Tasks
1. **Sketch the System**: Draw the system of two sheets, and include the coordinate system.
2. **Compute the Electric Field Vector using Superposition**:
- Use the principle of superposition, \( \mathbf{E} = \mathbf{E_1} + \mathbf{E_2} \), to find the electric field vector \( \mathbf{E} \) generated by the two sheets:
- (a) for \( y < 0 \)
- (b) for \( 0 < y < d \)
- (c) for \( d < y \)
3. **Plot Electric Field Components**: Plot \( E_x \), \( E_y \), \( E_z \) and \( |\mathbf{E}| = \sqrt{E_x^2 + E_y^2 + E_z^2} \) as a function of \( y \).
This exercise explores the properties of electric fields in the presence of charged flat sheets and applies the superposition principle to calculate the net field.
Expert Solution
Step 1
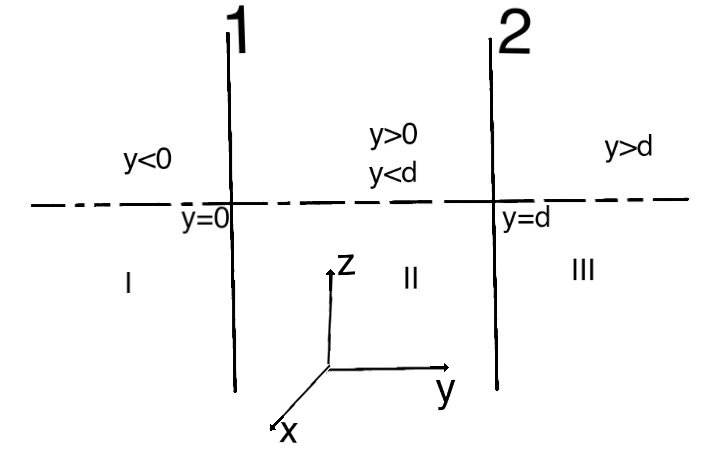
Given two sheets are placed at y=0 and y=d
The sketch of the given system:
Trending now
This is a popular solution!
Step by step
Solved in 6 steps with 9 images
