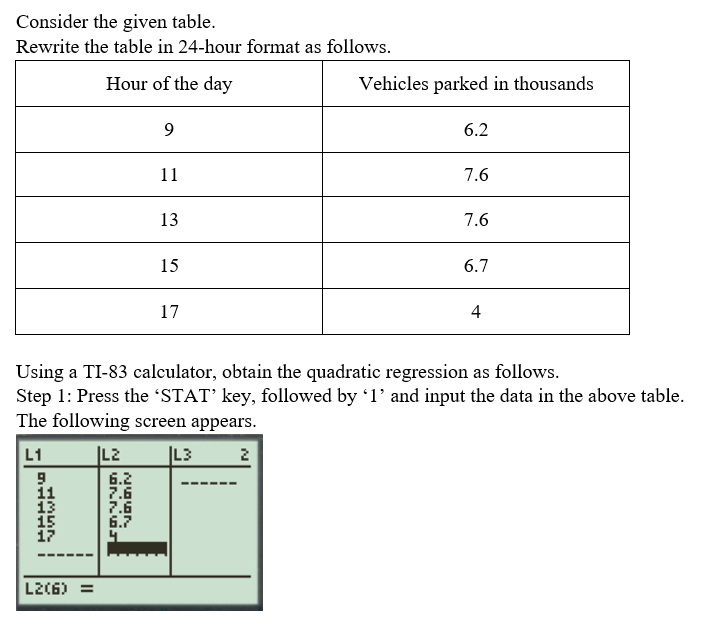
The table below shows the number, in thousands, of vehicles parked in the central business district of a certain city on a typical Friday as a function of the hour of the day. Hour of the day Vehicles parked (thousands) 9 A.M. 6.2 11 A.M. 7.6 1 P.M. 7.6 3 P.M. 6.7 5 P.M. 4 (a) Use regression to find a quadratic model for the data. (Let V be the number of vehicles and t be the time in hours since midnight. Round the regression parameters to three decimal places.) V =
Correlation
Correlation defines a relationship between two independent variables. It tells the degree to which variables move in relation to each other. When two sets of data are related to each other, there is a correlation between them.
Linear Correlation
A correlation is used to determine the relationships between numerical and categorical variables. In other words, it is an indicator of how things are connected to one another. The correlation analysis is the study of how variables are related.
Regression Analysis
Regression analysis is a statistical method in which it estimates the relationship between a dependent variable and one or more independent variable. In simple terms dependent variable is called as outcome variable and independent variable is called as predictors. Regression analysis is one of the methods to find the trends in data. The independent variable used in Regression analysis is named Predictor variable. It offers data of an associated dependent variable regarding a particular outcome.
The table below shows the number, in thousands, of vehicles parked in the central business district of a certain city on a typical Friday as a function of the hour of the day.
| Hour of the day | Vehicles parked (thousands) |
|---|---|
| 9 A.M. | 6.2 |
| 11 A.M. | 7.6 |
| 1 P.M. | 7.6 |
| 3 P.M. | 6.7 |
| 5 P.M. | 4 |
Step by step
Solved in 2 steps with 2 images









