The optimal solution of this linear programming problem is at the intersection of constraints 1 and 2. Max 3x1 + x2 s.t. 4x1 + x2 ≤ 400 4x1 + 3x2 ≤ 600 x1 + 2x2 ≤ 300 x1, x2 ≥ 0 Over what range can the coefficient of x1 vary before the current solution is no longer optimal? (Round your answers to two decimal places.) Over what range can the coefficient of x2 vary before the current solution is no longer optimal? (Round your answers to two decimal places.) Compute the dual value for the first constraint? Compute the dual value for the second constraint? Compute the dual value for the third constraint?
The optimal solution of this linear programming problem is at the intersection of constraints 1 and 2. Max 3x1 + x2 s.t. 4x1 + x2 ≤ 400 4x1 + 3x2 ≤ 600 x1 + 2x2 ≤ 300 x1, x2 ≥ 0 Over what range can the coefficient of x1 vary before the current solution is no longer optimal? (Round your answers to two decimal places.) Over what range can the coefficient of x2 vary before the current solution is no longer optimal? (Round your answers to two decimal places.) Compute the dual value for the first constraint? Compute the dual value for the second constraint? Compute the dual value for the third constraint?
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
The optimal solution of this linear programming problem is at the intersection of constraints 1 and 2.
Max 3x1 + x2
| s.t. | ||||
| 4x1 + x2 | ≤ | 400 | ||
| 4x1 + 3x2 | ≤ | 600 | ||
| x1 + 2x2 | ≤ | 300 | ||
| x1, x2 | ≥ | 0 |
Over what range can the coefficient of x1 vary before the current solution is no longer optimal? (Round your answers to two decimal places.)
Over what range can the coefficient of x2 vary before the current solution is no longer optimal? (Round your answers to two decimal places.)
Compute the dual value for the first constraint?
Compute the dual value for the second constraint?
Compute the dual value for the third constraint?
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 4 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
need correct answers. The ones here are incorrect
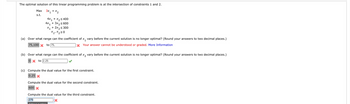
Transcribed Image Text:The optimal solution of this linear programming problem is at the intersection of constraints 1 and 2.
Max
3x₁ + x₂
s.t.
4x₁ + x₂ ≤ 400
4x₁ + 3x₂ ≤600
X₁ + 2x₂ ≤ 300
X1 X₂20
(a) Over what range can the coefficient of x₁ vary before the current solution is no longer optimal? (Round your answers to two decimal places.)
to 75,
x Your answer cannot be understood or graded. More Information
75,100
(b) Over what range can the coefficient of x₂ vary before the current solution is no longer optimal? (Round your answers to two decimal places.)
0x to 2.25
(c) Compute the dual value for the first constraint.
0.25 X
Compute the dual value for the second constraint.
600 X
Compute the dual value for the third constraint.
275
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

