Homework Help is Here – Start Your Trial Now!
Engineering
Mechanical Engineering
The length of the unit vector AB has a magnitude of _____ m.

The length of the unit vector AB has a magnitude of _____ m.

Elements Of Electromagnetics
Elements Of Electromagnetics
7th Edition
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Sadiku, Matthew N. O.
ChapterMA: Math Assessment
Section: Chapter Questions
Problem 1.1MA
See similar textbooks
icon
Related questions
Question

The length of the unit vector AB has a magnitude of _____ m.

choice would be the vector AC. sion r x F for the moment of a 1 to take moments directly about any any point on the line of action of the the A-components indicate that they 3 The negative signs associated with shown on the free-body diagram. tion in this problem is the freedom is a vector from the moment center to permits the choice of an axis that axis. In this problem this freedom 2 Recall that the vectorr in the expres- 2.5 m 3 m 4.5 m 152 Chapter 3 Equilibrium The welded tubular frame is segured to the horizontal x-y plane by a ban- and-socket joint at A and receives support from the loose-fitting ring at B. Under the action of the 2-kN load, rotation about a line from A to B is prevented by the cable CD, and the frame is stable in the position shown. Neglect the weight of the frame compared with the applied load and determine the tension T in the cable, the reaction at the ring, and the reaction components at A. SAMPLE PROBLEM 3/7 2 kN 6 m 2.5 m А Solufion. The system is clearly three-dimensional with no lines or planes of symmetry, and therefore the problem must be analyzed as a general space sys- tem of forces. The free-body diagram is drawm, where the ring reaction is shown in terms of its two components. All unknowns except T may be eliminated by a moment sum about the line AB. The direction of AB is specified by the unit (4.5j + 6k) = (3j + 4k). The moment of T about AB 1 m y E Bx 1 1 vector n = Te F= 2 kN is the component in the direction of AB of the vector moment about the point A and equals r1 × T.n. Similarly the moment of the applied load F about AB is r2 x F.n. With CD = /46.2 m, the vector expressions for T, F, r1, and r2 are V62 + 4.52 bet/ B2 r2 n T. (2i + 2.5j – 6k) 46.2 F = 2j kN %3D T = Ay. %3D D\ 2) ri = -i + 2.5j m r, = 2.5i + 6k m Az The moment equation now becomes В T [EMAB = 0] (-i+ 2.5j) x (2i + 2.5j – 6k) (3j + 4k) 46.2 АВ T1 T.n + (2.5i + 6k) × (2j) (3j + 4k) = 0 %3D rị xT Completion of the vector operations gives 48T + 20 = 0 T = 2.83 kN Ans. -y | 46.2 and the components of T become Helpful Hints T = 0.833 kN T, = 1.042 kN T, = -2.50 kN 1 The advantage of using vector nota- We may find the remaining unknowns by moment and force summations as follows: permits the choice of an axis that eliminates five of the unknowns. [EM, = 0] 2(2.5) – 4.5B, - 1.042(3) = 0 %3D B, = 0.417 kN %3D [EM, = 0] 4.5B, - 2(6) – 1.042(6) = 0 Ans. B, = 4.06 kN %3D [EF, = 0] A, + 0.417 + 0.833 = 0 Ans. force A, = -1.250 kN 3 EF, = 0] A, + 2 + 1.042 = 0 Ans. A, = -3.04 kN equally simple choice would be the vector AC. [EF, = 0] force. Instead of r1, an %3D A, + 4.06 – 2.50 = 0 Ans. A, = -1.556 kN Ans. those are in the opposite direction to shown on the free-body diagra
Transcribed Image Text:choice would be the vector AC. sion r x F for the moment of a 1 to take moments directly about any any point on the line of action of the the A-components indicate that they 3 The negative signs associated with shown on the free-body diagram. tion in this problem is the freedom is a vector from the moment center to permits the choice of an axis that axis. In this problem this freedom 2 Recall that the vectorr in the expres- 2.5 m 3 m 4.5 m 152 Chapter 3 Equilibrium The welded tubular frame is segured to the horizontal x-y plane by a ban- and-socket joint at A and receives support from the loose-fitting ring at B. Under the action of the 2-kN load, rotation about a line from A to B is prevented by the cable CD, and the frame is stable in the position shown. Neglect the weight of the frame compared with the applied load and determine the tension T in the cable, the reaction at the ring, and the reaction components at A. SAMPLE PROBLEM 3/7 2 kN 6 m 2.5 m А Solufion. The system is clearly three-dimensional with no lines or planes of symmetry, and therefore the problem must be analyzed as a general space sys- tem of forces. The free-body diagram is drawm, where the ring reaction is shown in terms of its two components. All unknowns except T may be eliminated by a moment sum about the line AB. The direction of AB is specified by the unit (4.5j + 6k) = (3j + 4k). The moment of T about AB 1 m y E Bx 1 1 vector n = Te F= 2 kN is the component in the direction of AB of the vector moment about the point A and equals r1 × T.n. Similarly the moment of the applied load F about AB is r2 x F.n. With CD = /46.2 m, the vector expressions for T, F, r1, and r2 are V62 + 4.52 bet/ B2 r2 n T. (2i + 2.5j – 6k) 46.2 F = 2j kN %3D T = Ay. %3D D\ 2) ri = -i + 2.5j m r, = 2.5i + 6k m Az The moment equation now becomes В T [EMAB = 0] (-i+ 2.5j) x (2i + 2.5j – 6k) (3j + 4k) 46.2 АВ T1 T.n + (2.5i + 6k) × (2j) (3j + 4k) = 0 %3D rị xT Completion of the vector operations gives 48T + 20 = 0 T = 2.83 kN Ans. -y | 46.2 and the components of T become Helpful Hints T = 0.833 kN T, = 1.042 kN T, = -2.50 kN 1 The advantage of using vector nota- We may find the remaining unknowns by moment and force summations as follows: permits the choice of an axis that eliminates five of the unknowns. [EM, = 0] 2(2.5) – 4.5B, - 1.042(3) = 0 %3D B, = 0.417 kN %3D [EM, = 0] 4.5B, - 2(6) – 1.042(6) = 0 Ans. B, = 4.06 kN %3D [EF, = 0] A, + 0.417 + 0.833 = 0 Ans. force A, = -1.250 kN 3 EF, = 0] A, + 2 + 1.042 = 0 Ans. A, = -3.04 kN equally simple choice would be the vector AC. [EF, = 0] force. Instead of r1, an %3D A, + 4.06 – 2.50 = 0 Ans. A, = -1.556 kN Ans. those are in the opposite direction to shown on the free-body diagra
Expert Solution
Step 1

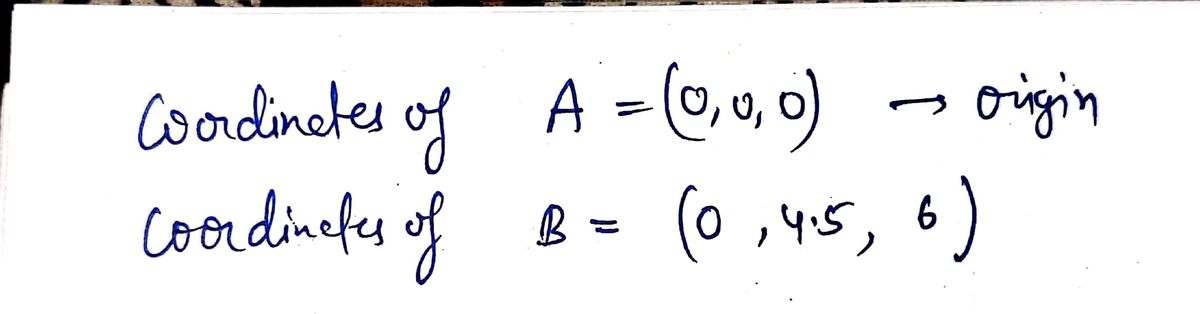
Mechanical Engineering homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Knowledge Booster
Basic Mechanics Problems
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.
Recommended textbooks for you
Elements Of Electromagnetics
Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press
Mechanics of Materials (10th Edition)
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON
Thermodynamics: An Engineering Approach
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education
Control Systems Engineering
Control Systems Engineering
Mechanical Engineering
ISBN:
9781118170519
Author:
Norman S. Nise
Publisher:
WILEY
Mechanics of Materials (MindTap Course List)
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:
9781337093347
Author:
Barry J. Goodno, James M. Gere
Publisher:
Cengage Learning
Engineering Mechanics: Statics
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:
9781118807330
Author:
James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:
WILEY
SEE MORE TEXTBOOKS