The heights of adult women in the US are normally distributed with a mean of 64 inches and a standard deviation of 3 inches. Find the minimum and maximum heights that represent the middle 50% of women’s heights. Include a sketch. Round to the nearest integer and include units in your answer
The heights of adult women in the US are
Solution:
Let the random variable X denotes the height of an adult woman in the U.S. It is given that the heights of adult women in the US are normally distributed with a mean of 64 inches and a standard deviation of 3 inches.
The minimum and maximum heights that represent the middle 50% of women's heights are required.
The total area under the normal probability curve is 1. The middle area is given t be 50% which is 0.50.
Thus, the remaining area is 1-0.50 = 0.50 which is equally distributed in the two tails of the curve. That means, there is 25% area to each (left and right) side of the middle 50% area. It is shown in the graph given below:
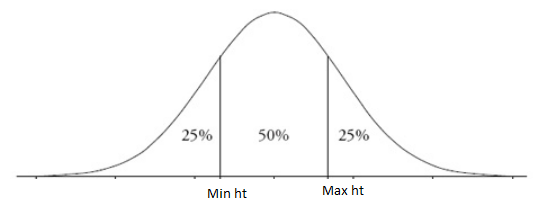
Where, Min ht means minimum height and Max ht means maximum height.
Step by step
Solved in 2 steps with 2 images









