The data below is from a random sample of married women drawn from the population of an urban area in a less-developed country. This data has two variables; 'a’ is the age at which each woman was married for the first time, 'b’ is whether or not at least one of their parents had a secondary or higher education (0=no, 1=yes). 1) Estimate the sample mean, variance, standard deviation, and standard error for age at first marriage for the entire population. Calculate the 95% confidence interval around this estimate and interpret. 2) Repeat the analysis from 1) above for each parental education group (*b’) separately. Do the confidence intervals overlap? 3) We hypothesize that children of more educated parents will marry later than children of less well educated parents. Perform a two-sample t-test of this hypothesis, using the folowing formula (the standard error for a two sample t-test combines the standard errors of each group) and interpret your result. Group l'will be those whose parents had more education, group '2' will be those whose parents had less. X1 – X2 t = + n1 n2


We have,
n = 30
n1 = n2 = 15
We compute the mean, variance, standard deviation and standard error for age at first marriage for the entire population.
We first compute the mean variance and standard deviation using excel formula as below:
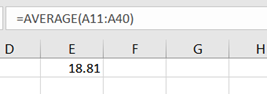
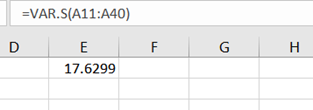
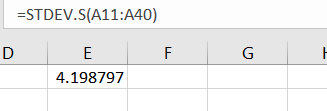
Thus, we have,
Mean = 18.81
Variance = 17.6299
Standard deviation = 4.198797.
Standard error = Standard deviation/√n = 4.198797/√30 = 0.766592.
The 95% confidence interval for population mean for age at first marriage for the entire population is computed as,
Thus, the 95% confidence interval for population mean for age at first marriage for the entire population is (17.23214, 20.36786)
The 95% confidence interval for population mean indicates that there is 95% chance that the true population will be contained in this interval.
Trending now
This is a popular solution!
Step by step
Solved in 6 steps with 9 images









