Answered: The coefficient of variation CV…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Question

The coefficient of variation CV describes the standard deviation as a percent of the mean. Because it has no units, you can use the coefficient of variation to compare data with different units. Find the coefficient of variation for each sample data set. What can you conclude?

CV= Standard Deviation/Mean Times 100

Heights Weights
68 205
76 193
75 221
70 227
70 200
80 221
79 189
73 184
72 199
70 173
70 211
68 203

CVheight=

CVweight=

Definition Definition Measure of central tendency that is the average of a given data set. The mean value is evaluated as the quotient of the sum of all observations by the sample size. The mean, in contrast to a median, is affected by extreme values. Very large or very small values can distract the mean from the center of the data. Arithmetic mean: The most common type of mean is the arithmetic mean. It is evaluated using the formula: μ = 1 N ∑ i = 1 N x i Other types of means are the geometric mean, logarithmic mean, and harmonic mean. Geometric mean: The nth root of the product of n observations from a data set is defined as the geometric mean of the set: G = x 1 x 2 ... x n n Logarithmic mean: The difference of the natural logarithms of the two numbers, divided by the difference between the numbers is the logarithmic mean of the two numbers. The logarithmic mean is used particularly in heat transfer and mass transfer. ln x 2 − ln x 1 x 2 − x 1 Harmonic mean: The inverse of the arithmetic mean of the inverses of all the numbers in a data set is the harmonic mean of the data. 1 1 x 1 + 1 x 2 + ...

Expert Solution

Step 1

Given information-

We have given the data of heights and weights.

We have to calculate the coefficient of variation of each data set.

The calculation of mean and standard deviation of each data set is given below.

	Heights	Weights
	68	205
	76	193
	75	221
	70	227
	70	200
	80	221
	79	189
	73	184
	72	199
	70	173
	70	211
	68	203
Sum	871	2426
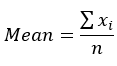	72.5833	202.167
Standard deviation	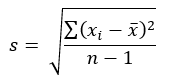4.07784	16.1405