dR dt dF dt 2(1-7) ¹ R-RF -16F +4RF
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Generate a slope field in that shows the solution curve in the RF-plane (rabbit/fox) for the system of predator-prey equations with initial conditions R(0)=8 and F(0)=1

Transcribed Image Text:This image contains a system of differential equations, likely modeling a biological or ecological process. The equations are:
1. \(\frac{dR}{dt} = 2 \left(1 - \frac{R}{3}\right)R - RF\)
2. \(\frac{dF}{dt} = -16F + 4RF\)
These equations describe how two variables, \(R\) and \(F\), change over time (\(t\)).
- The first equation models the rate of change of \(R\). It includes a term \(2 \left(1 - \frac{R}{3}\right)R\), which is likely a logistic growth term affected by the presence of \(F\). This suggests that \(R\) might represent a population with natural growth and some interaction with \(F\).
- The second equation models the rate of change of \(F\). The term \(-16F\) suggests \(F\) might have a high rate of decay or death, while \(4RF\) indicates interaction with \(R\), possibly a consumptive relationship.
This system can be used to study interactions such as predator-prey dynamics, competition, or symbiosis. Analyzing these equations can provide insights into the stability and behavior of the modeled system over time.
Expert Solution
Step 1
Given system of equation:
To find:
The solution of the given system.
Draw the slope field.
Step by step
Solved in 7 steps with 1 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
That is not what I needed. I needed a FIGURE, a SLOPE FIELD given the initial conditions. Possibly generated with geogebra application
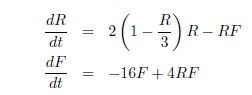
Transcribed Image Text:dR
dt
dF
dt
2(1-B) ¹
R-RF
-16F +4RF
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

