Test the claim about the population mean, µ, at the given level of significance using the given sample statistic Claim: μ#6000; α=0.07; o=389. Sample statistics: x=6200, n = 35 Identify the null and alternative hypotheses. Choose the correct answer below. OA. Ho μ-6000 Ha: μ#6000 OC. Ho μ#6000 H₂ μ = 6000 *** E. Ho: ²6000 H₂ μ#6000 O B. Ho μ≤6000 Ha μ#6000 O D. Ho μ#6000 Hg: με 6000 OF. Ho #6000 H₂ μ≤6000
Test the claim about the population mean, µ, at the given level of significance using the given sample statistic Claim: μ#6000; α=0.07; o=389. Sample statistics: x=6200, n = 35 Identify the null and alternative hypotheses. Choose the correct answer below. OA. Ho μ-6000 Ha: μ#6000 OC. Ho μ#6000 H₂ μ = 6000 *** E. Ho: ²6000 H₂ μ#6000 O B. Ho μ≤6000 Ha μ#6000 O D. Ho μ#6000 Hg: με 6000 OF. Ho #6000 H₂ μ≤6000
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question

Transcribed Image Text:Test the claim about the population mean, u, at the given level of significance using the given sample statistics.
Claim: #6000; α=0.07; = 389. Sample statistics: x=6200, n=35
μ
Identify the null and alternative hypotheses. Choose the correct answer below.
Ο A. Ho: μ = 6000
Ha: µ#6000
OC. Ho µ‡ 6000
H₂ μ=6000
QE. Ho: 26000
H₂: μ#6000
OB. Ho u≤6000
Ha μ#6000
O D. Ho: μ#6000
Hai μ ≥6000
OF. Ho μ#6000
H₂ μ≤6000
11
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps with 1 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
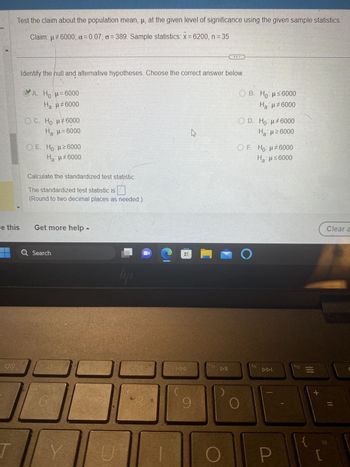
Transcribed Image Text:Test the claim about the population mean, µ, at the given level of significance using the given sample statistics.
Claim: μ#6000; a= 0.07; a=389. Sample statistics: x = 6200, n = 35
e this
70
Identify the hull and alternative hypotheses. Choose the correct answer below.
A. H=6000
Ha: µ‡6000
OC. Ho: μ‡6000
H₂:µ=6000
O E. Ho: µ ≥6000
Ha:µ‡6000
Calculate the standardized test statistic.
The standardized test statistic is
(Round to two decimal places as needed.)
Get more help -
Q Search
6
lipi
DC
U
98
J
ESDEN
tg
pag
8
বিব
DE
9
M
f10
DII
ⒸB. Ho: μ≤6000
Ha: μ‡6000
OD. Ho: μ#6000
Ha: μ ≥6000
OF. Ho: μ#6000
Ha: μ≤6000
O
f11
DDI
P
f12
1!1
+
Clear a
=
Solution
Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman