t I Exercise A.5 (B) Show that y = 3a²x-³ is strictly increasing for a < x 2a. Hint: put x = 2a cosh o and use the relation cosh³ = (cosh 30+3 cosh o)/4.
t I Exercise A.5 (B) Show that y = 3a²x-³ is strictly increasing for a < x 2a. Hint: put x = 2a cosh o and use the relation cosh³ = (cosh 30+3 cosh o)/4.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
100%
How about part c?

Transcribed Image Text:8:04 PM Sat 16 Sep
X
<
00
00
M820 ✓
Ans
(a)
P
So
00
Exercise A.5 (B) Show that y = 3a²x - x³ is strictly increasing for −a < x < a
and that on this interval y increases from -2a³ to 2a³.
m820_solutions_itm50...
→
be
By putting a = 2a sino and using the identity sin³ 6 = (3 sin 6 – sin 36)/4, show
that the equation becomes
y = 2a³ sin 30 and hence that (y) = 2a sin
(203)).
(c) Find the inverse for x > 2a. Hint: put x = 2a cosho and use the relation cosh³ =
(cosh 30 + 3 cosh o)/4.
0
A function is increasing if f'ox xo.
(X)
y² = 3a² - 3x² >0
a + x > 0
-a
x > -a
So the interval
0
T
>
$
→
increases
y
<x< a the function is increasing.
f(a) < foxo < feas
-2a²³ < y < 2a²³
m820_mn2_itm50992...
→ (a-x) (a+x) >o
a-x>0
a > x
sin-1
83%
from -2a³ to 2a³.
↑

Transcribed Image Text:B
y
Since
=
6a³ sin & - 8 a³ sin ³ &
баз
= 2a²³ (3 sin & -4 sin ³0)
=
2
11
So y = 20²³ sin 34
sin 3p =
介
=>
3a²x - x³
3
3a² (2a sin 4) - (2a sin 8)³
↑
↑
3
2a³ sin (34)
34
X =
$
=
y
2a³
sin"
_x cys =
I sin
m
(3)
2a sin &
La sin ( — Sin" Las)
= Ja sin ( — sin¹ = 13)
Expert Solution
Step 1: Describing the part c)
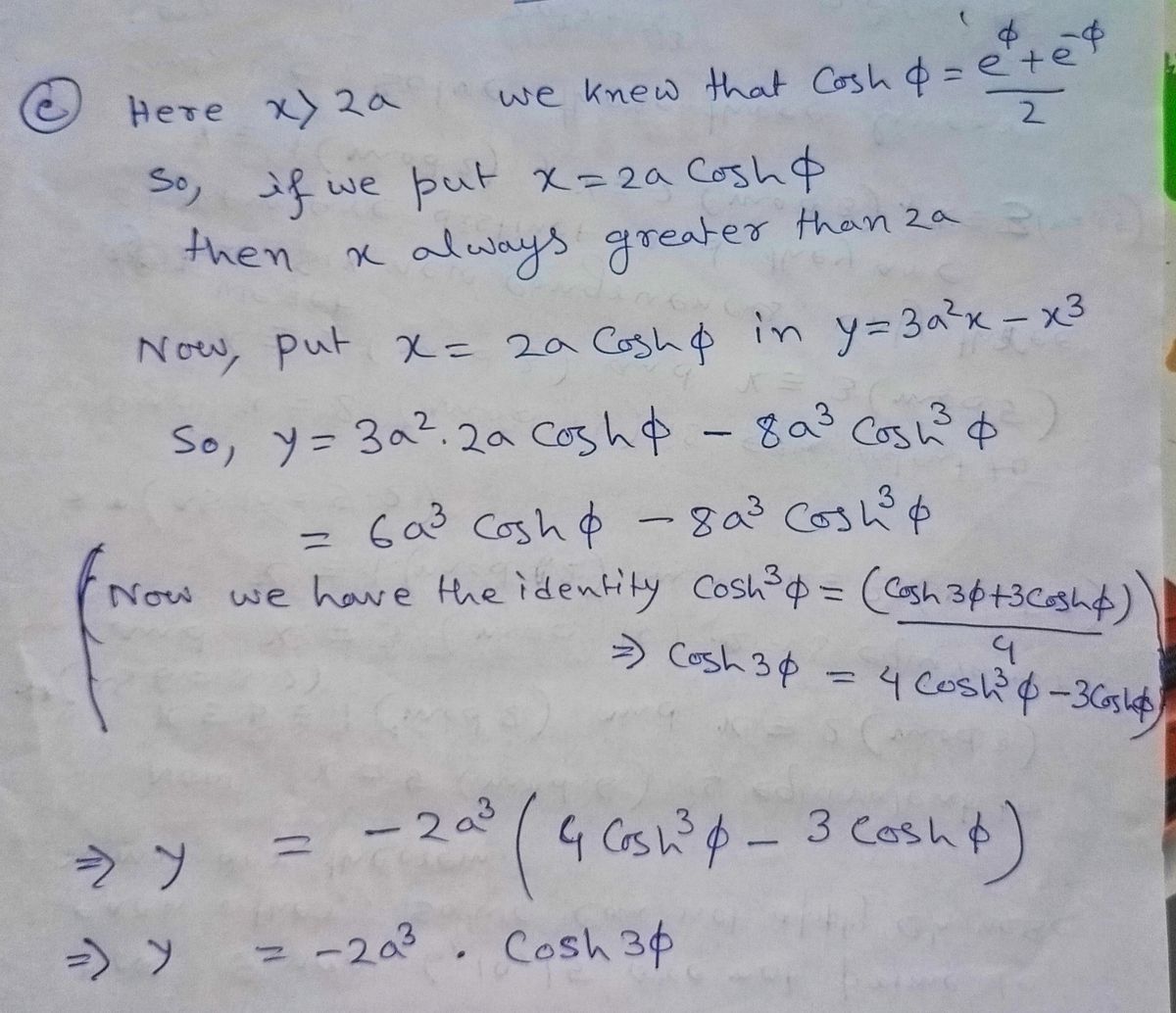
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

