Suppose a there is a 40% chance a randomly selected person likes strawberry ice cream, a 70% chance a randomly selected person likes chocolate ice cream, and a 25% chance that a randomly selected person likes both strawberry and chocolate ice cream. What is the probability a randomly selected person likes chocolate ice cream but not strawberry? What is the probability a randomly selected person likes neither chocolate nor strawberry ice cream?
Contingency Table
A contingency table can be defined as the visual representation of the relationship between two or more categorical variables that can be evaluated and registered. It is a categorical version of the scatterplot, which is used to investigate the linear relationship between two variables. A contingency table is indeed a type of frequency distribution table that displays two variables at the same time.
Binomial Distribution
Binomial is an algebraic expression of the sum or the difference of two terms. Before knowing about binomial distribution, we must know about the binomial theorem.
Suppose a there is a 40% chance a randomly selected person likes strawberry ice cream, a 70% chance a randomly selected person likes chocolate ice cream, and a 25% chance that a randomly selected person likes both strawberry and chocolate ice cream.
- What is the
probability a randomly selected person likes chocolate ice cream but not strawberry? - What is the probability a randomly selected person likes neither chocolate nor strawberry ice cream?
(1)
Obtain the probability that a randomly selected person likes chocolate ice cream but not strawberry.
The probability that a randomly selected person likes chocolate ice cream but not strawberry is obtained below as follows:
Let A denote the event or probability that the selected person likes strawberry ice cream. That is, P(A)=0.40.
Let B denote the event or probability that the selected person likes Chocolate ice cream. That is, P(B)=0.70.
Let (A intersection B) denote the event of probability that selected person likes both strawberry and chocolate ice cream. That is, P(A intersection B)=0.25.
The required probability is,
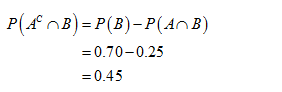
Thus, the probability that randomly selected person likes chocolate ice cream but not strawberry is 0.45.
Step by step
Solved in 2 steps with 2 images









