Suppose a quality control expert examines iterms for defects in a series of independent fixates, each of a fixed duration, and suppose that defects are present. Let p be the probability that the defect or flaw is detected and 1-p the probability that a defect or flaw is not detected. Let the r.v. X = the number of defects detected in n fixations. a. What is the pmf of X? b. What is the expected value of X = E(X)? c. What is the moment generating function (mgf) for the r.v. X (Remember to state the interval of validity for t)? d. Use it to find the Variance of X.
Suppose a quality control expert examines iterms for defects in a series of independent fixates, each of a fixed duration, and suppose that defects are present. Let p be the
a. What is the pmf of X?
b. What is the
c. What is the moment generating
d. Use it to find the Variance of X.
Hello. Since your question has multiple sub-parts, we will solve first three sub-parts for you. If you want remaining sub-parts to be solved, then please resubmit the whole question and specify those sub-parts you want us to solve.
It is given that an expert is examining items in a series of independent fixates. p is the probability that the item is defected and detected while 1-p is the probability that an item is defect but does not detected.
Consider that X is a random variable defined as the number of detected in n fixations.
Thus,

a)
The p.m.f of X can be defined as:
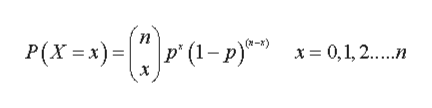
Step by step
Solved in 4 steps with 4 images




