Strength of concrete: The compressive strength, in kilopascals, was measured for concrete blocks from five different batches of concrete, both three and six days after pouring. The data are as follows. Can you conclude that the mean strength after three days is greater than the mean strength after six days? Let μ₁ represent the mean strength after three days and μμ₁-₂. Use the a= 0.05 level and the critical value method with the table. Block 1 2 3 4 5 1384 1341 1386 1382 1349 After 3 days After 6 days 1344 1343 1307 1325 1301 Send data to Excel Part 1 of 5 (a) State the null and alternate hypotheses. Hồi Ha=0| H₁: Pa> This hypothesis test is a right-tailed test. Part: 1 / 5 Part 2 of 5 Find the critical value. Round the answer to three decimal places. If there is more than one critical value, separate them with commas. The critical value(s): X
Strength of concrete: The compressive strength, in kilopascals, was measured for concrete blocks from five different batches of concrete, both three and six days after pouring. The data are as follows. Can you conclude that the mean strength after three days is greater than the mean strength after six days? Let μ₁ represent the mean strength after three days and μμ₁-₂. Use the a= 0.05 level and the critical value method with the table. Block 1 2 3 4 5 1384 1341 1386 1382 1349 After 3 days After 6 days 1344 1343 1307 1325 1301 Send data to Excel Part 1 of 5 (a) State the null and alternate hypotheses. Hồi Ha=0| H₁: Pa> This hypothesis test is a right-tailed test. Part: 1 / 5 Part 2 of 5 Find the critical value. Round the answer to three decimal places. If there is more than one critical value, separate them with commas. The critical value(s): X
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question

Transcribed Image Text:Strength of concrete: The compressive strength, in kilopascals, was measured for concrete blocks from five different batches of concrete, both three and six
days after pouring. The data are as follows. Can you conclude that the mean strength after three days is greater than the mean strength after six days? Let μ₁
represent the mean strength after three days and μμ₁ −μ₂. Use the a= 0.05 level and the critical value method with the table.
Block
1
2
3
4
5
After 3 days
1386
1382 1349
1384 1341
After 6 days 1344 1343 1307 1325
1301
Send data to Excel
Part 1 of 5
(a) State the null and alternate hypotheses.
Ho|ua = 0
H₁ H₂ > 0
This hypothesis test is a right-tailed ▼test.
Part: 1 / 5
Part 2 of 5
Find the critical value. Round the answer to three decimal places. If there is more than one critical value, separate them with commas.
The critical value(s):
0.0....
X
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
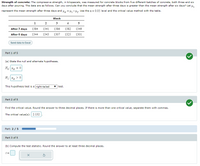
Transcribed Image Text:Strength of concrete: The compressive strength, in kilopascals, was measured for concrete blocks from five different batches of concrete, both three and six
days after pouring. The data are as follows. Can you conclude that the mean strength after three days is greater than the mean strength after six days? Let μ₁
represent the mean strength after three days and μμ₁ −μ₂. Use the a= 0.05 level and the critical value method with the table.
Block
1
2
3
4
5
After 3 days
1341 1386
1382
1349
1384
1344 1343 1307
After 6 days
1325 1301
Send data to Excel
Part 1 of 5
(a) State the null and alternate hypotheses.
Ho: Ha = 0
H₁: Pa
This hypothesis test is a right-tailed
test.
Part 2 of 5
Find the critical value. Round the answer to three decimal places. If there is more than one critical value, separate them with commas.
The critical value(s): 2.132
Part: 2 / 5
Part 3 of 5
(b) Compute the test statistic. Round the answer to at least three decimal places.
t=
X
Solution
Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman