Solve 2 cos (t) – 7 cos(t) – 4 0 for all solutions 0
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
There are 4 decimals answers needed for x
![**Problem:**
Solve the equation \(2 \cos^2(t) - 7 \cos(t) - 4 = 0\) for all solutions \(0 \leq t < 2\pi\).
**Instructions:**
Find the values of \(t\) and provide your answers accurate to 2 decimal places, listed and separated by commas.
**Solution:**
1. **Equation Setup:**
- The equation is quadratic in form with respect to \(\cos(t)\).
- Let \(x = \cos(t)\). The equation becomes \(2x^2 - 7x - 4 = 0\).
2. **Solve the Quadratic Equation:**
- Use the quadratic formula \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\), where \(a = 2\), \(b = -7\), and \(c = -4\).
- Calculate the discriminant: \(b^2 - 4ac = (-7)^2 - 4 \times 2 \times (-4) = 49 + 32 = 81\).
- Solve for \(x\):
\[
x = \frac{7 \pm \sqrt{81}}{4}
\]
\[
x = \frac{7 \pm 9}{4}
\]
- The solutions for \(x\) are:
\[
x_1 = \frac{16}{4} = 4
\]
\[
x_2 = \frac{-2}{4} = -0.5
\]
3. **Find \(t\) for Each \(x\):**
- The cosine function is bounded by \([-1, 1]\), so \(x_1 = 4\) is not possible. We only consider \(x_2 = -0.5\).
- Find \(t\) such that \(\cos(t) = -0.5\) within the interval \(0 \leq t < 2\pi\).
- Solutions for \(\cos(t) = -0.5\) are \(t = \frac{2\pi}{3}\) and \(t = \frac{4\pi}{3}\).
4. **Final Answer:**
- The](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F306f2d1a-9f72-422e-b433-8de8d735b303%2Fcb718527-f287-46bc-8765-378fdb3a55a3%2Fo3ovjm_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem:**
Solve the equation \(2 \cos^2(t) - 7 \cos(t) - 4 = 0\) for all solutions \(0 \leq t < 2\pi\).
**Instructions:**
Find the values of \(t\) and provide your answers accurate to 2 decimal places, listed and separated by commas.
**Solution:**
1. **Equation Setup:**
- The equation is quadratic in form with respect to \(\cos(t)\).
- Let \(x = \cos(t)\). The equation becomes \(2x^2 - 7x - 4 = 0\).
2. **Solve the Quadratic Equation:**
- Use the quadratic formula \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\), where \(a = 2\), \(b = -7\), and \(c = -4\).
- Calculate the discriminant: \(b^2 - 4ac = (-7)^2 - 4 \times 2 \times (-4) = 49 + 32 = 81\).
- Solve for \(x\):
\[
x = \frac{7 \pm \sqrt{81}}{4}
\]
\[
x = \frac{7 \pm 9}{4}
\]
- The solutions for \(x\) are:
\[
x_1 = \frac{16}{4} = 4
\]
\[
x_2 = \frac{-2}{4} = -0.5
\]
3. **Find \(t\) for Each \(x\):**
- The cosine function is bounded by \([-1, 1]\), so \(x_1 = 4\) is not possible. We only consider \(x_2 = -0.5\).
- Find \(t\) such that \(\cos(t) = -0.5\) within the interval \(0 \leq t < 2\pi\).
- Solutions for \(\cos(t) = -0.5\) are \(t = \frac{2\pi}{3}\) and \(t = \frac{4\pi}{3}\).
4. **Final Answer:**
- The
Expert Solution
Step 1
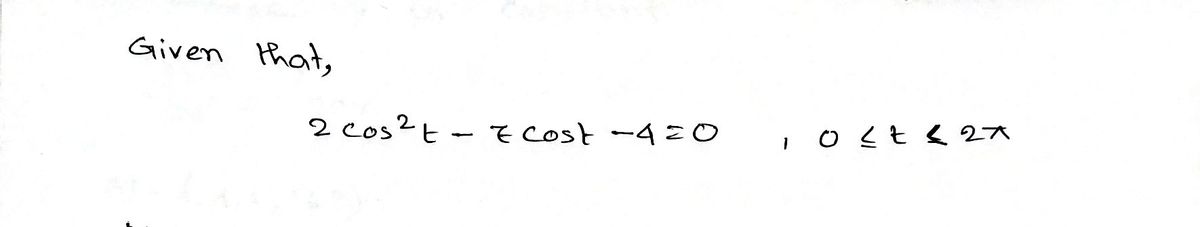
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning