Show that the average square momentum for a free particle whose wavefunction is V (x) = Aeikɛ (3.1) is k?h?. Hint: Notice that V(x) = AŲ„(x). For normalization A° | dæV„(x)*V_(x) = 1 (3.2) so that A² = 1/ | drV_„(x)*V_¬(x) (3.3) Then use < p >= [ dr¥(x)*p%¥ (x).
Show that the average square momentum for a free particle whose wavefunction is V (x) = Aeikɛ (3.1) is k?h?. Hint: Notice that V(x) = AŲ„(x). For normalization A° | dæV„(x)*V_(x) = 1 (3.2) so that A² = 1/ | drV_„(x)*V_¬(x) (3.3) Then use < p >= [ dr¥(x)*p%¥ (x).
Related questions
Question
how to get this problem?
thank you!

Transcribed Image Text:Show that the average square momentum < p > for a free particle
whose wavefunction is
V (x)
= Aeika
(3.1)
is k?h?.
Hint: Notice that V(x) = AV¬(x). For normalization
| dæ|¥ (x)|° = A² / dæV¬(x)*V¬(x) = 1
(3.2)
so that
A² = 1/ | dæV=(x)*V_(x)
fa
(3.3)
Then use < p, >=
[ dx¥(x)*p¿¥(x).
Expert Solution
Step 1
In this case, the wave function and its complex conjugate are given in the following way.

Assumption:
The particle is free to move in the interval (a, b).
On using equations (1) and (2), the wave function is normalized in the following way.
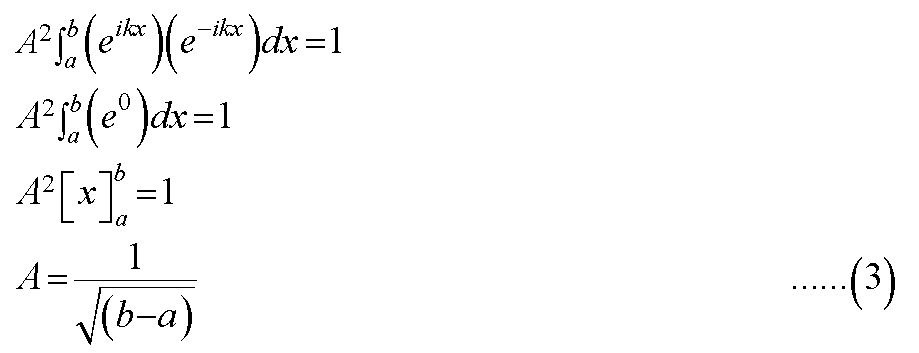
Therefore, from equations (1), (2), and (3), we have,

Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 5 images
