### Hypothesis Testing on Women's Height**Scenario:**Several years ago, the mean height of women aged 20 years or older was 63.7 inches. A recent random sample of 45 women aged 20 or older shows a mean height of 64.1 inches. ### Questions and Explanation:**(a) State the appropriate null and alternative hypotheses to assess whether women are taller today.**Choose from the following options:- **A.** \( H_0: \mu = 64.1 \text{ in.} \) versus \( H_1: \mu \neq 64.1 \text{ in.} \)- **B.** \( H_0: \mu = 63.7 \text{ in.} \) versus \( H_1: \mu \neq 63.7 \text{ in.} \)- **C.** \( H_0: \mu = 63.7 \text{ in.} \) versus \( H_1: \mu < 63.7 \text{ in.} \)- **D.** \( H_0: \mu = 64.1 \text{ in.} \) versus \( H_1: \mu < 64.1 \text{ in.} \)- **E.** \( H_0: \mu = 63.7 \text{ in.} \) versus \( H_1: \mu > 63.7 \text{ in.} \)- **F.** \( H_0: \mu = 64.1 \text{ in.} \) versus \( H_1: \mu > 64.1 \text{ in.} \)**(b) Suppose the P-value for this test is 0.11. Explain what this value represents.**The P-value of 0.11 indicates that, assuming the null hypothesis \( H_0 \) is true, there is an 11% probability of obtaining a sample mean of 64.1 inches or more extreme by random chance.**(c) Write a conclusion for this hypothesis test assuming an \( \alpha = 0.05 \) level of significance.**Since the P-value of 0.11 is greater than the significance level \( \alpha \) of 0.05, we do not reject the

Population mean sample size n= 45sample mean = 64.1

Several years ago, the mean height of women 20 years of age or older was 63.7 inches. Suppose that a random sample of 45 women who are 20 years of age or older today results in a mean height of 64.1 inches (a) State the appropriate null and alternative hypotheses to assess whether women are taller today. (b) Suppose the P-value for this test is 0.11. Explain what this value represents. (c) Write a conclusion for this hypothesis test assuming an a= 0.05 level of significance. (a) State the appropriate null and alternative hypotheses to assess whether women are taller today. OA. H=64.1 in versus H, µ/64.1 in. OC. Ho H=63.7 in versus H, p<63.7 in. OE. Ho p=63.7 in versus H, p> 63.7 in. CITT OB. Ho u 63.7 in versus H, #63.7 in OD. Ho H=64.1 in versus H, p<64.1 in. OF. Hou 64.1 in versus H, µ> 64.1 in.

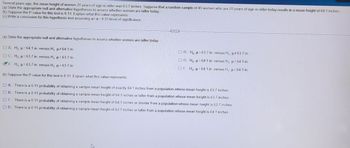
Several years ago, the mean height of women 20 years of age or older was 63.7 inches. Suppose that a random sample of 45 women who are 20 years of age or older today results in a mean height of 64.1 inches (a) State the appropriate null and alternative hypotheses to assess whether women are taller today. (b) Suppose the P-value for this test is 0.11. Explain what this value represents. (c) Write a conclusion for this hypothesis test assuming an a= 0.05 level of significance. (a) State the appropriate null and alternative hypotheses to assess whether women are taller today. OA. H=64.1 in versus H, µ/64.1 in. OC. Ho H=63.7 in versus H, p<63.7 in. OE. Ho p=63.7 in versus H, p> 63.7 in. CITT OB. Ho u 63.7 in versus H, #63.7 in OD. Ho H=64.1 in versus H, p<64.1 in. OF. Hou 64.1 in versus H, µ> 64.1 in.

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Similar questions

The director of research and development is testing a new drug. She wants to know if there is evidence at the 0.05 level that the drug stays in the system for more than 352 minutes. For a sample of 54 patients the mean time the drug stayed in the system was 360 minutes. Assume the population standard deviation is 25. Find the p-value of the test statistic
A population of values has a normal distribution with random sample of size n = 164. μ = 81.9 and σ = 75.7. You intend to draw a Find P89, which is the score separating the bottom 89% scores from the top 11% scores. P89 (for single values) = Find P89, which is the mean separating the bottom 89% means from the top 11% means. P89 (for sample means) = Enter your answers as numbers accurate to 1 decimal place. **********NOTE************ round your answer to ONE digit after the decimal point! **** Answers obtained using exact z-scores or z-scores rounded to 3 decimal places are accepted.
Fran is training for her first marathon, and she wants to know if there is a significant difference between the mean number of miles run each week by group runners and individual runners who are training for marathons. She interviews 42 randomly selected people who train in groups and finds that they run a mean of 47.1 miles per week. Assume that the population standard deviation for group runners is known to be 4.4 miles per week. She also interviews a random sample of 47 people who train on their own and finds that they run a mean of 48.5 miles per week. Assume that the population standard deviation for people who run by themselves is 1.8 miles per week. Test the claim at the 0.01 level of significance. Let group runners training for marathons be Population 1 and let individual runners training for marathons be Population 2. Step 2 of 3 : Compute the value of the test statistic. Round your answer to two decimal places.
Nabisco claims that Chip Ahoy Cookies have an x ̅=28.67 chocolate chips per cookie with a SD=2.67. You randomly select 36 cookies from a new bag and carefully remove all the chocolate chips from each of the 36 cookies. You find the mean of the chocolate chips for the 36 cookies is 24.27 chocolate chips per cookie. Calculate the standard error for the chocolate chips in your experiment. (round to the nearest hundredth).
A researcher wishes to estimate the frue proportion of all speeders who exceed the posted speed limit on a particular stretch of road in the Canyonlands National Park where there are frequent accidents. How large should the sample be so that with 97 percent confidence, the sample proportion will not differ from the true proportion by more than 0.311?
A researcher wishes to estimate the true proportion of all speeders who exceed the posted speed limit on a particular stretch of road in the Canyonlands National Park where there are frequent accidents. How large should the sample be so that with 91 percent confidence, the sample proportion will not differ from the true proportion by more than 0.261?z = n ⩾
The mean age of bus drivers in chicago is 56.7 years. If a hypothesis test is performed, how should you interpret a decision that rejects the null hypothesis?
A bottled water distributor wants to determine whether the mean amount of water contained in 1-gallon bottles purchased from a nationally known water bottling company is actually 1 gallon. You know from the water bottling company specifications that the standard deviation of the amount of water is 0.02 gallon. You select a random sample of 50 bottles, and the mean amount of water per 1-gallon bottle is 0.992 gallon. What is the test statistic?
The principal at Riverside High School would like to estimate the mean length of time each day that it takes all the buses to arrive and unload the students. What is the minimum sample size needed if the principal would like to be 90% confident that the sample mean is off by, at most, 2 minutes. Assume that standard deviation is 14 minutes. (Approximate the final answer)
In the US, the average one-way commuting time is 26.4 minutes. Is this different in Atlanta? One survey of 35 Atlanta commuters found an average one-way commuting time of 30.7 minutes. (a) The test statistic is 1.1846. What is the meaning of this test statistic? The average error between different sample results and the hypothesized mean is 1.1846.The current sample result is 1.1846 standard errors above the hypothesized mean. The maximum error between different sample results and the hypothesized mean is 1.1846. (b) Based on the test statistic of 1.1846, what is the p-value to test if the average commuting time in Atlanta is different than the rest of the US? (4 decimals.) (c) On the basis of the above p-value, what can be said regarding a 95% confidence interval for the true average commuting time? The interval contain the value 26.4, because this value . (d) Suppose the sample size was increased to 120 Atlanta commuters, with other values remaining the same. How would…