Rules of the Game Using the notation that was introduced in the Crowdmark question for this part, write in symbolic form (first order logic) the three rules of the game explained in English below: a) A player wins the game if and only if the other player loses (i.e. doesn't win) the b) game. game. If, during a player's turn, that player takes all the coins in the pile, they will lose the c) After a player takes k coins from a pile of n coins during their turn (where k
Rules of the Game Using the notation that was introduced in the Crowdmark question for this part, write in symbolic form (first order logic) the three rules of the game explained in English below: a) A player wins the game if and only if the other player loses (i.e. doesn't win) the b) game. game. If, during a player's turn, that player takes all the coins in the pile, they will lose the c) After a player takes k coins from a pile of n coins during their turn (where k
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:Rules of the Gamo
Using the notation that was introduced in the Crowdmark question for this part, write in symbolic
form (first order logic) the three rules of the game explained in English below:
a)
A player wins the game if and only if the other player loses (i.e. doesn't win) the
b)
game.
game.
K
If, during a player's turn, that player takes all the coins in the pile, they will lose the
c)
After a player takes k coins from a pile of n coins during their turn (where k<n), then
it is the other player's turn to remove coins from a pile of n-k coins
Problem Statement
The conjecture that you will be proving is stated in English as: "if it is a player's turn to take coins
from a pile of n coins, and both players play the best strategy possible, then this player will win the
game if and only if n mod 4 is not 1."
This conjecture needs to be expressed symbolically in the form VnEN* P(n).
d)
Write the predicate function P(n) in symbolic form. Note that what P(n) describes is
about any player, and this needs to be integrated in the symbolic form for P(n).

Transcribed Image Text:Game
Question 2, which is in three parts, centers around a two-player game with very simple rules:
This game starts with a pile of n coins. The two players take turns removing coins from the pile, either 1, 2, or 3
coins at a time. The player removing the last coin loses.
You will prove by strong induction that if each player plays the best strategy possible, the first player will win if n
mod 4 € (0, 2, 3) and the second player will win if n mod 4 = 1.
Formalization
Before you do so, you will need to formalize the rules of the game and the conjecture you will be proving. The
following notation is defined to support this process in Part 1 and your proof in Parts 2 and 3:
• The two players are elements of the set A={0,1}. I.e. one of them is player 0 and the other is player 1. This
notation is useful because if you call one player p, then the other is simply 1-p
Three predicate functions are provided: turn, take, and wins:
●
o For any player p in A and any n in N, turn(p,n) means that it is the turn of player p to remove 1, 2, or 3
coins from a pile of n coins
o For any player p in A and any m in N, take(p,m) means that player p takes m coins from the pile of coins
o For any player p in A, wins(p) means that player p will win the game if both players play the best strategy
possible
Finally, you can also use the % notation for mod if you want: a mod b can be written as a % b
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Answer this questions
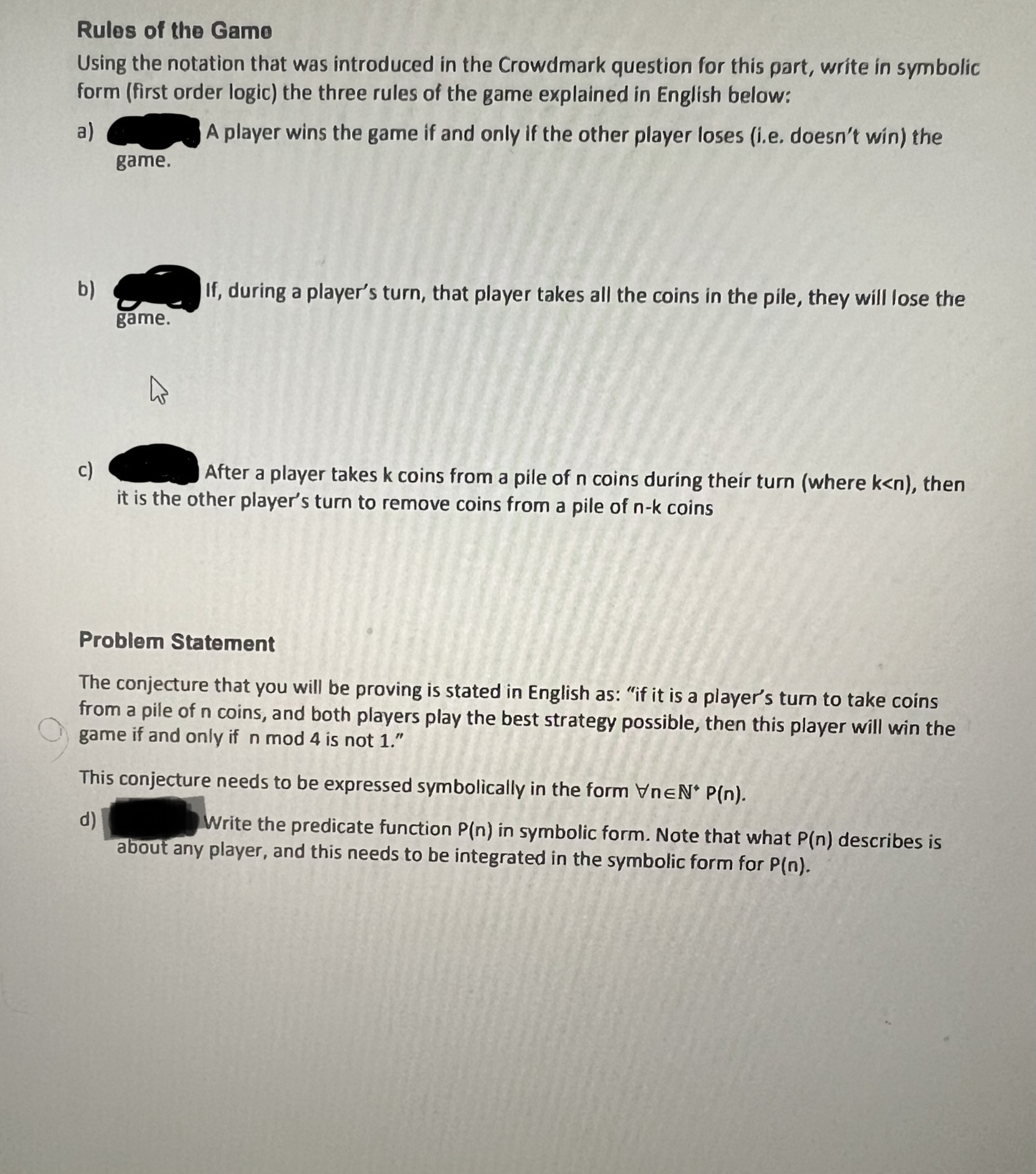
Transcribed Image Text:Rules of the Gamo
Using the notation that was introduced in the Crowdmark question for this part, write in symbolic
form (first order logic) the three rules of the game explained in English below:
a)
A player wins the game if and only if the other player loses (i.e. doesn't win) the
b)
game.
game.
K
If, during a player's turn, that player takes all the coins in the pile, they will lose the
c)
After a player takes k coins from a pile of n coins during their turn (where k<n), then
it is the other player's turn to remove coins from a pile of n-k coins
Problem Statement
The conjecture that you will be proving is stated in English as: "if it is a player's turn to take coins
from a pile of n coins, and both players play the best strategy possible, then this player will win the
game if and only if n mod 4 is not 1."
This conjecture needs to be expressed symbolically in the form VnEN* P(n).
d)
Write the predicate function P(n) in symbolic form. Note that what P(n) describes is
about any player, and this needs to be integrated in the symbolic form for P(n).
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

