Resistors for electronic circuits are manufactured on a high-speed automated machine. The machine is set up to produce a large run of resistors of 1,000 ohms each. Use Exhibit 10.13. To set up the machine and to create a control chart to be used throughout the run, 15 samples were taken with four resistors in each sample. The complete list of samples and their measured values are as follows: Use three-sigma control limits. SAMPLE NUMBER READINGS (IN OHMS) 1016 1024 990 1018 1030 1016 992 1028 1030 986 1006 1016 1015 986 981 1 2 3 995 981 991 991 1025 1028 1001 1012 1015 1002 972 1007 1017 995 1002 1002 1013 995 1023 988 1020 1019 998 1020 985 4 1013 985 1005 991 1014 975 975 1004 1003 1013 1011 1002 987 980 1008 1020 1005 1004 8 10 11 12 13 14 15 1014 1015 a. Calculate the mean and range for the above samples. (Round "Mean" to 2 decimal places and "Range" to the nearest whole number.) Sample Number Mean Range 1 2 3 6 8 10 11 12 13 14 15 b. Determine X and R. (Round your answers to 3 decimal places.)
Resistors for electronic circuits are manufactured on a high-speed automated machine. The machine is set up to produce a large run of resistors of 1,000 ohms each. Use Exhibit 10.13. To set up the machine and to create a control chart to be used throughout the run, 15 samples were taken with four resistors in each sample. The complete list of samples and their measured values are as follows: Use three-sigma control limits. SAMPLE NUMBER READINGS (IN OHMS) 1016 1024 990 1018 1030 1016 992 1028 1030 986 1006 1016 1015 986 981 1 2 3 995 981 991 991 1025 1028 1001 1012 1015 1002 972 1007 1017 995 1002 1002 1013 995 1023 988 1020 1019 998 1020 985 4 1013 985 1005 991 1014 975 975 1004 1003 1013 1011 1002 987 980 1008 1020 1005 1004 8 10 11 12 13 14 15 1014 1015 a. Calculate the mean and range for the above samples. (Round "Mean" to 2 decimal places and "Range" to the nearest whole number.) Sample Number Mean Range 1 2 3 6 8 10 11 12 13 14 15 b. Determine X and R. (Round your answers to 3 decimal places.)
Practical Management Science
6th Edition
ISBN:9781337406659
Author:WINSTON, Wayne L.
Publisher:WINSTON, Wayne L.
Chapter2: Introduction To Spreadsheet Modeling
Section: Chapter Questions
Problem 20P: Julie James is opening a lemonade stand. She believes the fixed cost per week of running the stand...
Related questions
Question

Transcribed Image Text:# Manufacturing Resistors for Electronic Circuits
Resistors for electronic circuits are manufactured on a high-speed automated machine. The machine is set up to produce a large run of resistors of 1,000 ohms each. To set up the machine and create a control chart to be used throughout the run, 15 samples were taken with four resistors in each sample. The measurements are used with three-sigma control limits.
## Sample Data
The following table shows the sample number and the readings for each sample in ohms:
| Sample Number | Readings (in Ohms) |
|---------------|------------------------|
| 1 | 1016, 995, 991, 1028 |
| 2 | 1024, 951, 991, 1001 |
| 3 | 909, 1015, 1025, 1012 |
| 4 | 918, 1002, 975, 995 |
| 5 | 1030, 1007, 1013, 1002 |
| 6 | 1016, 1015, 968, 1002 |
| 7 | 992, 1001, 1011, 1013 |
| 8 | 1028, 991, 1002, 995 |
| 9 | 1030, 1014, 987, 1023 |
| 10 | 986, 975, 998, 988 |
| 11 | 1006, 975, 1008, 1020 |
| 12 | 1016, 1004, 1020, 1019 |
| 13 | 1015, 1023, 1025, 995 |
| 14 | 986, 1013, 1004, 1020 |
| 15 | 981, 1014, 1015, 985 |
## Calculations
a. Calculate the **mean** and **range** for the above samples.
- Round the **Mean** to 2 decimal places.
- Round the **Range** to the nearest whole number.
| Sample Number | Mean | Range |
|---------------|------|-------|
| 1 | |

Transcribed Image Text:### Statistical Process Control Instructions
#### c. Determine the UCL and LCL for a \(\bar{X}\)-Chart.
- **Instructions:** Round your answers to 3 decimal places.
- **Inputs Required:**
- UCL (Upper Control Limit)
- LCL (Lower Control Limit)
#### d. Determine the UCL and LCL for R-Chart.
- **Instructions:** Leave no cells blank - be certain to enter "0" wherever required. Round your answers to 3 decimal places.
- **Inputs Required:**
- UCL (Upper Control Limit)
- LCL (Lower Control Limit)
#### e. What comments can you make about the process?
- **Options:**
- ○ The process is in statistical control.
- ○ The process is out of statistical control.
### Explanation of Diagrams
- **\(\bar{X}\)-Chart and R-Chart Tables:**
- Each table consists of two rows labeled "UCL" and "LCL" for entering the Upper Control Limit and Lower Control Limit values respectively.
These tools help in understanding variations in a process and determining whether it is statistically controlled or not. The \(\bar{X}\)-Chart monitors the mean of a process, while the R-Chart monitors the range of process variability.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 5 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Resistors for electronic circuits are manufactured on a high-speed automated machine. The machine is set up to produce a large run of resistors of 1,000 ohms each. Use Exhibit 13.7.
To set up the machine and to create a control chart to be used throughout the run, 15 samples were taken with four resistors in each sample. The complete list of samples and their measured values are as follows: Use three-sigma control limits.
c. Determine the UCL and LCL for a X−X− chart. (Round your answers to 3 decimal places.)
d. Determine the UCL and LCL for R-chart. (Leave no cells blank - be certain to enter "0" wherever required. Round your answers to 3 decimal places.)
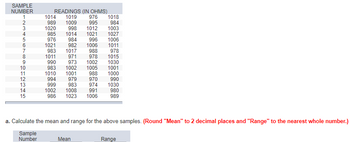
Transcribed Image Text:SAMPLE
NUMBER
1
234567890112 13 14 15
READINGS (IN OHMS)
1019
1009
998
1014
984
Sample
Number
1014
989
1020
985
976
1021
983
1011
990
983
982
1017
971
973
1010 1001
994
979
999 983
1002 1008
976
995
1002 1005 1001
1000
1018
984
1003
1012
1021
996
1006
988
978
978 1015
1002
1030
Mean
988
970
974
1027
1006
1011
991
980
986 1023 1006 989
990
1030
a. Calculate the mean and range for the above samples. (Round "Mean" to 2 decimal places and "Range" to the nearest whole number.)
Range
Solution
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, operations-management and related others by exploring similar questions and additional content below.Recommended textbooks for you

Practical Management Science
Operations Management
ISBN:
9781337406659
Author:
WINSTON, Wayne L.
Publisher:
Cengage,

Operations Management
Operations Management
ISBN:
9781259667473
Author:
William J Stevenson
Publisher:
McGraw-Hill Education

Operations and Supply Chain Management (Mcgraw-hi…
Operations Management
ISBN:
9781259666100
Author:
F. Robert Jacobs, Richard B Chase
Publisher:
McGraw-Hill Education

Practical Management Science
Operations Management
ISBN:
9781337406659
Author:
WINSTON, Wayne L.
Publisher:
Cengage,

Operations Management
Operations Management
ISBN:
9781259667473
Author:
William J Stevenson
Publisher:
McGraw-Hill Education

Operations and Supply Chain Management (Mcgraw-hi…
Operations Management
ISBN:
9781259666100
Author:
F. Robert Jacobs, Richard B Chase
Publisher:
McGraw-Hill Education


Purchasing and Supply Chain Management
Operations Management
ISBN:
9781285869681
Author:
Robert M. Monczka, Robert B. Handfield, Larry C. Giunipero, James L. Patterson
Publisher:
Cengage Learning

Production and Operations Analysis, Seventh Editi…
Operations Management
ISBN:
9781478623069
Author:
Steven Nahmias, Tava Lennon Olsen
Publisher:
Waveland Press, Inc.