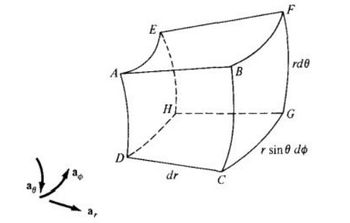
Refer to Figure below; disregard the differential lengths and imagine that the object is part of a spherical shell. It may be described as 3 ≤ r ≤ 5, 60° ≤ θ ≤ 90°, 45° ≤ ø ≤ 60° where surface r = 3 is the same as AEHD, surface θ = 60° is AEFB, and surface ø = 45° is ABCD. Calculate: The surface area AEHD
Refer to Figure below; disregard the differential lengths and imagine that the object is part of a spherical shell. It may be described as 3 ≤ r ≤ 5, 60° ≤ θ ≤ 90°, 45° ≤ ø ≤ 60° where surface r = 3 is the same as AEHD, surface θ = 60° is AEFB, and surface ø = 45° is ABCD. Calculate:
The surface area AEHD

Trending now
This is a popular solution!
Step by step
Solved in 2 steps

Refer to Figure below; disregard the differential lengths and imagine that the object is part of a spherical shell. It may be described as 3 ≤ r ≤ 5, 60° ≤ θ ≤ 90°, 45° ≤ ø ≤ 60° where surface r = 3 is the same as AEHD, surface θ = 60° is AEFB, and surface ø = 45° is ABCD.
Calculate:
The surface area ABCD
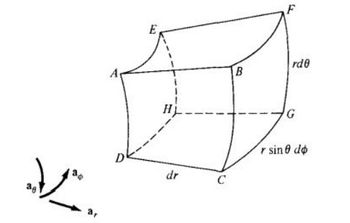
Refer to the Figure below; disregard the differential lengths and imagine that the object is part of a spherical shell. It may be described as 3 ≤ r ≤ 5, 60° ≤ θ ≤ 90°, 45° ≤ ø ≤ 60° where surface r = 3 is the same as AEHD, surface θ = 60° is AEFB, and surface ø = 45° is ABCD.
Calculate:
The distance DH
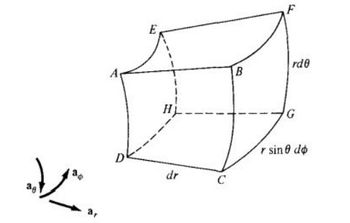
Refer to the Figure below; disregard the differential lengths and imagine that the object is part of a spherical shell. It may be described as 3 ≤ r ≤ 5, 60° ≤ θ ≤ 90°, 45° ≤ ø ≤ 60° where surface r = 3 is the same as AEHD, surface θ = 60° is AEFB, and surface ø = 45° is ABCD.
Calculate:
The volume of the object
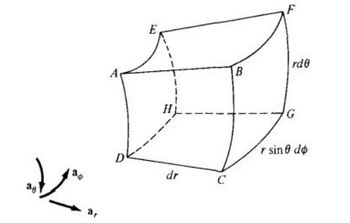
Refer to the Figure below; disregard the differential lengths and imagine that the object is part of a spherical shell. It may be described as 3 ≤ r ≤ 5, 60° ≤ θ ≤ 90°, 45° ≤ ø ≤ 60° where surface r = 3 is the same as AEHD, surface θ = 60° is AEFB, and surface ø = 45° is ABCD.
Calculate:
The distance FG