Answered: Random samples of two species of iris…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Topic Video

Question

Random samples of two species of iris gave the following petal lengths (in cm).

x₁, Iris virginica	5.2	5.9	4.5	4.9	5.7	4.8	5.8	6.4	5.7	5.9
x₂, Iris versicolor	4.5	4.9	4.7	5.0	3.8	5.1	4.4	4.2

Find the value of the chi-square statistic for the sample. (Round your answer to two decimal places.)

What are the degrees of freedom?

(b) Find a 90% confidence interval for the population standard deviation of

x₁.

(Round your answers to two decimal places.)

lower limit
upper limit

Find the value of the sample F statistic. (Round your answer to two decimal places.)

Expert Solution

Step 1

Given data provides random samples of two species of iris gave the following petal lengths (in cm).

Mean & standard deviation for x₁, Iris virginica :

The sample size is $n = 10$ . The provided sample data along with the data required to compute the sample mean $\bar{X}$ and sample variance $s^{2}$ are shown in the table below:

	X	X²
	5.2	27.04
	5.9	34.81
	4.5	20.25
	4.9	24.01
	5.7	32.49
	4.8	23.04
	5.8	33.64
	6.4	40.96
	5.7	32.49
	5.9	34.81
Sum =	54.8	303.54

The sample mean $\bar{X}$ is computed as follows:

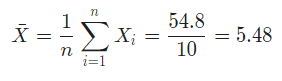
Also, the sample variance $s^{2}$ is

Therefore, the sample standard deviation $s$ is

Mean & standard deviation for x₂, Iris versicolor :

The sample size is $n = 8$ . The provided sample data along with the data required to compute the sample mean $\bar{X}$ and sample variance $s^2$ are shown in the table below:

	X	X²
	4.5	20.25
	4.9	24.01
	4.7	22.09
	5	25
	3.8	14.44
	5.1	26.01
	4.4	19.36
	4.2	17.64
Sum =	36.6	168.8

The sample mean $\bar{X}$ is computed as follows:

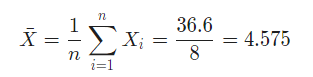
Also, the sample variance $s^{2}$ is

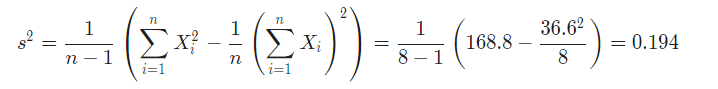
Therefore, the sample standard deviation $s$ is

Step 2

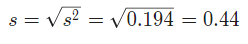
The provided sample variance is $s^2 = 0.6$ and the sample size is given by $n = 10$ .

Null and Alternative Hypotheses

The following null and alternative hypotheses need to be tested:

$Ho: \sigma^2 = 0.3025$

$Ha: \sigma^2 > 0.3025$

This corresponds to a right-tailed test, for which a Chi-Square test for one population variance will be used.

Rejection Region

Based on the information provided, the significance level is $\alpha = 0.05$ , and the the rejection region for this right-tailed test is $R = \{\chi^2: \chi^2 > 16.919\}$ .

Test Statistics

The Chi-Squared statistic is computed as follows:

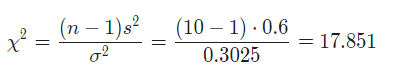
Decision about the null hypothesis

Since it is observed that $χ^{2} = 17.851 > χ_{U 2} = 16.919$ , it is then concluded that the null hypothesis is rejected.

Conclusion

It is concluded that the null hypothesis Ho is rejected. Therefore, there is enough evidence to claim that the population variance $σ^{2}$ is greater than 0.3025, at the 0.05 significance level.

Step by step

Solved in 4 steps with 10 images

Knowledge Booster

$Hypothesis Tests and Confidence Intervals for Means$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Similar questions