Question: During the days of coronavirus, people work most of the time from home. Many offices, schools, universities conduct their works, meetings, classes online. As a result of this new normal, it is assumed that on average, utility expenses per family (electricity, water, gas etc.) increases by 40% per month. For the verification of this assumption, four months data of percentage change of utility expenses of 10 families of similar size is given below and answer the following questions, the data is normally distributed: Percentage change of utility expenses April 33.65 37.09 29.72 33.42 38.14 34.9 37.35 38.66 22.92 34.19 May 37.19 36.61 40.35 28.19 35.19 37.43 38.03 42.99 30.22 38.8 June 37.13 36.2 43.6 35.31 33.66 28.51 37.67 20.68 38.04 38.43 July 38.84 32.17 34.9 30.17 29.63 27.14 32.17 33.46 36.72 39.64 Which statistical technique(s) will be suitable for testing this assumption? (Only write the name(s) of all possible techniques) Write tabulated value of test statistic at0.05 level of significance Write the null and alternative hypothesis for this test. Write your final conclusion about the assumption. What will be the 95% confidence interval for the average percentage change of utility expenses on the basis of given data.

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Concept explainers

Question

Question: During the days of coronavirus, people work most of the time from home. Many offices, schools, universities conduct their works, meetings, classes online. As a result of this new normal, it is assumed that on average, utility expenses per family (electricity, water, gas etc.) increases by 40% per month. For the verification of this assumption, four months data of percentage change of utility expenses of 10 families of similar size is given below and answer the following questions, the data is normally distributed:

	Percentage change of utility expenses
April	33.65	37.09	29.72	33.42	38.14	34.9	37.35	38.66	22.92	34.19
May	37.19	36.61	40.35	28.19	35.19	37.43	38.03	42.99	30.22	38.8
June	37.13	36.2	43.6	35.31	33.66	28.51	37.67	20.68	38.04	38.43
July	38.84	32.17	34.9	30.17	29.63	27.14	32.17	33.46	36.72	39.64

Which statistical technique(s) will be suitable for testing this assumption? (Only write the name(s) of all possible techniques)
Write tabulated value of test statistic at0.05 level of significance
Write the null and alternative hypothesis for this test.
Write your final conclusion about the assumption.
What will be the 95% confidence interval for the average percentage change of utility expenses on the basis of given data.

Features Features Normal distribution is characterized by two parameters, mean (µ) and standard deviation (σ). When graphed, the mean represents the center of the bell curve and the graph is perfectly symmetric about the center. The mean, median, and mode are all equal for a normal distribution. The standard deviation measures the data's spread from the center. The higher the standard deviation, the more the data is spread out and the flatter the bell curve looks. Variance is another commonly used measure of the spread of the distribution and is equal to the square of the standard deviation.

Expert Solution

Step 1 Answer and Explanation:

(1) ANOVA- One Way Classification and Completely Randomised Design are the statistical techniques will be suitable for testing this assumption.

(3) Objective: To test whether the percentage change of utility expenses in four months are significant or not.

Setting of Hypothesis:

Null Hypothesis H₀ : Four months data of percentage change of utility expenses of 10 families are equal. that is, H₀ : μ₁ = μ₂ = ... = μ₁₀.

Alternative Hypothesis H₁ : Four months data of percentage change of utility expenses of 10 families are not equal. that is, H₁ : μ₁≠ μ₂≠ ... ≠ μ₁₀.

Calculation:

Given table is as follows below:

Now, Grand Total (G) = ΣTi = 1389.11 Raw Sum of Squares (RSS) = ΣΣy_ij² = 33.65² + 37.09²+ 29.72² + ... + 39.64² = 49177 Correction Factor (CF) = G²/N = (1389.11)²/40 = 48240.66 Total Sum of Squares (TSS) = RSS - CF = 49177 - 48240.66 = 936.34 Treatment Sum of Squares (SST) = Σ Ti²/n_i - CF= 48293.16 - 48240.66 = 52.5 Error Sum of Squares (ESS) = TSS - SST = 936.34 - 52.5 = 883.84

Step 2 Answer and Explanation:

Construction of ANOVA Table:

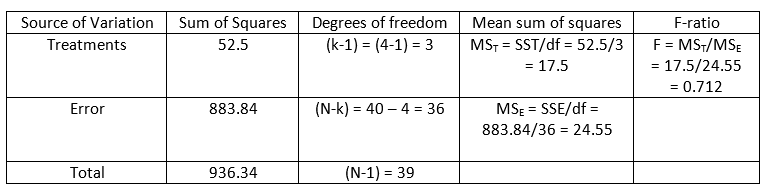
If F calculated value is 0.712 at 0.05 level of significance with (3,36) degrees of freedom then the F tabulated value is 2.866.

Since, F cal = 0.712 < F tab = 2.866. Hence, null hypothesis H₀ may be accepted at 5% level of significance with (3,36) degrees of freedom.

(2) The tabulated value of the test statistic is 2.866 at 0.05 level of significance.

(4) Conclusion: Therefore, from the above statistical evaluation we conclude that there is a strong evidence to accept the null hypothesis H₀. That means, four months data of percentage change of utility expenses of 10 families are equal.

Step by step

Solved in 3 steps with 2 images

Knowledge Booster

$Continuous Probability Distribution$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.