Question 4 Let a and b be natural numbers. Give all solutions to the following equation: 2ª + 1 = 6² Hint: Rewrite the above such that it talks about multiplication () instead of addition (+).
Question 4 Let a and b be natural numbers. Give all solutions to the following equation: 2ª + 1 = 6² Hint: Rewrite the above such that it talks about multiplication () instead of addition (+).
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:Question 4
Let a and b be natural numbers.
Give all solutions to the following equation:
2a + 1 = 6²
Hint: Rewrite the above such that it talks about multiplication () instead of addition (+).
Expert Solution
Step 1
Solution:
2a + 1 = b2
=> 2a = b2 - 1
= (b - 1)(b + 1)
=> both (b - 1) and (b + 1) are of the form 2k for some integers k.
i.e, b - 1 = 2m, say
b + 1 = 2n , say.
=> m + n = a
Also, 2m = 2n - 2
=> 2m = 2(2n-1 - 1)
=> 2m-1 = 2n-1 - 1
Step by step
Solved in 2 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
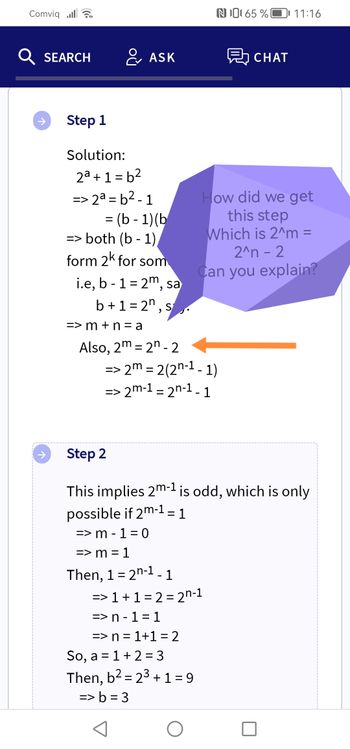
Transcribed Image Text:Comviqlar
Q SEARCH
Step 1
Solution:
20+1=b2
=
ASK
2a = b2 - 1
= (b -1) (b
=> both (b - 1)
form 2k for som
i.e, b - 1 = 2m, sa
b+1=2, s
=>m+n=a
Also, 2m 2n-2
N065 %
=> 2m = 2(2n-1-1)
=> 2m-1 = 2n-1 - 1
=> 1 + 1 = 2 = 2n-1
=> n-1=1
=> n = 1+1=2
So, a = 1 + 2 = 3
Then, b² = 2³ + 1 = 9
-
=> b=3
CHAT
How did we get
this step
Which is 2^m =
2^n - 2
Can you explain?
11:16
Step 2
This implies 2m-1 is odd, which is only
possible if 2m-1 = 1
=> m - 1 = 0
=> m = 1
Then, 1 = 2n-1 - 1
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

