Q4. The probability density function of the RV X is f(x) = 5e-kx for x ≥ 0. Find 2) bslubado ni a) the value of k. b) the probability that x>1. 0.67 Jerr 2oulou c) If Y~N(2,2). X and Y are independent, then find the P(0.25 ≤X ≤ 0.5 and 0.1 ≤Y ≤ 0). iw baworla) 126l edi vir sulsv vods art T sam of be
Q4. The probability density function of the RV X is f(x) = 5e-kx for x ≥ 0. Find 2) bslubado ni a) the value of k. b) the probability that x>1. 0.67 Jerr 2oulou c) If Y~N(2,2). X and Y are independent, then find the P(0.25 ≤X ≤ 0.5 and 0.1 ≤Y ≤ 0). iw baworla) 126l edi vir sulsv vods art T sam of be
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
![**Problem Statement:**
Q4. The probability density function of the random variable (RV) \( X \) is given by:
\[ f(x) = 5e^{-kx} \text{ for } x \geq 0. \]
**Tasks:**
a) Find the value of \( k \).
b) Find the probability that \( X > 1 \).
c) If \( Y \sim N(2,2) \), and \( X \) and \( Y \) are independent, then find the probability:
\[ P(0.25 \leq X \leq 0.5 \text{ and } 0.1 \leq Y \leq 0). \]
Note: The problem setup includes calculations related to probability distributions and assumes a foundational understanding of probability theory and statistics.
(Note: The image contains text and faint background diagrams that do not require detailed explanation, as they do not pertain to the problem statement described.)](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F3af11e6a-2a61-4302-a4ee-f3c4efdfe331%2F9cd28058-3ab6-4c7c-842b-68e6a0936e73%2F4nuqk59_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Q4. The probability density function of the random variable (RV) \( X \) is given by:
\[ f(x) = 5e^{-kx} \text{ for } x \geq 0. \]
**Tasks:**
a) Find the value of \( k \).
b) Find the probability that \( X > 1 \).
c) If \( Y \sim N(2,2) \), and \( X \) and \( Y \) are independent, then find the probability:
\[ P(0.25 \leq X \leq 0.5 \text{ and } 0.1 \leq Y \leq 0). \]
Note: The problem setup includes calculations related to probability distributions and assumes a foundational understanding of probability theory and statistics.
(Note: The image contains text and faint background diagrams that do not require detailed explanation, as they do not pertain to the problem statement described.)
Expert Solution
Step 1
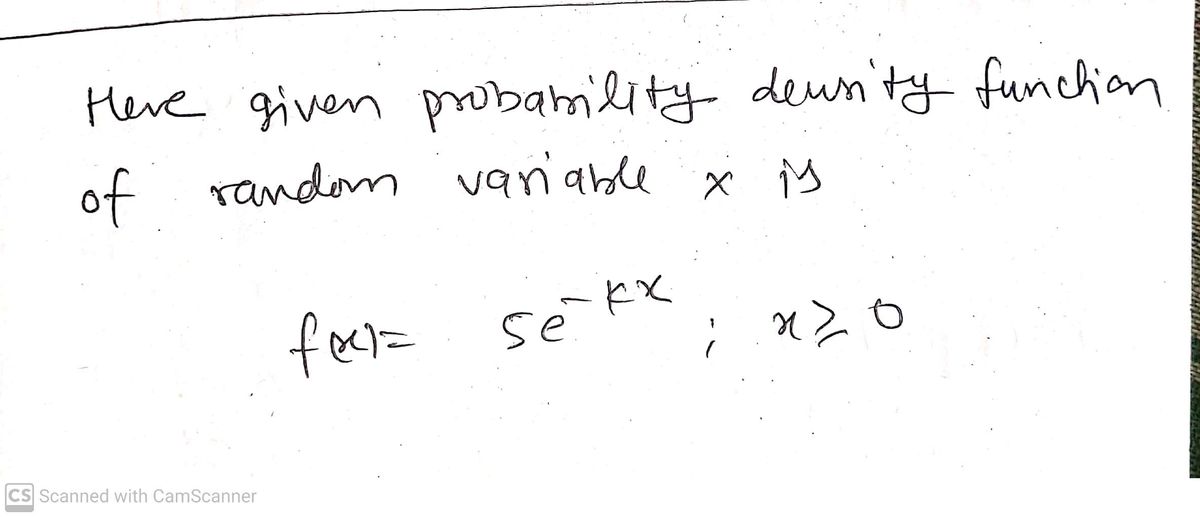
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
