2. The continuous random variables x and y have known joint probability density function f(x,y) given by x Osysxsl fxy(x,y) = y +1 0 otherwise where is a positive constant. a) Determine the value of the constant c that makes the above a valid joint probability density function. b) Using the result of part a), obtain now the marginal probability density function fx(x) of the random variable x. c) Using the result of part a), obtain now the marginal probability density function f(x) of the random variable y. d) Verify the results of parts b) and c) to make sure that the two probability density functions are valid. e) Are the two random variables statistically independent? f) Obtain the expected value E(XY).
2. The continuous random variables x and y have known joint probability density function f(x,y) given by x Osysxsl fxy(x,y) = y +1 0 otherwise where is a positive constant. a) Determine the value of the constant c that makes the above a valid joint probability density function. b) Using the result of part a), obtain now the marginal probability density function fx(x) of the random variable x. c) Using the result of part a), obtain now the marginal probability density function f(x) of the random variable y. d) Verify the results of parts b) and c) to make sure that the two probability density functions are valid. e) Are the two random variables statistically independent? f) Obtain the expected value E(XY).
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
![### Joint Probability Density Function of Continuous Random Variables
The continuous random variables \( X \) and \( Y \) have a known joint probability density function \( f_{XY}(x, y) \) given by:
\[
f_{XY}(x, y) =
\begin{cases}
\frac{c \cdot x}{y + 1} & \text{if } 0 \leq y \leq x \leq 1 \\
0 & \text{otherwise}
\end{cases}
\]
where \( c \) is a positive constant.
#### Tasks:
a) **Determine the value of the constant \( c \):**
Find \( c \) such that the function becomes a valid joint probability density function.
b) **Marginal Probability Density Function \( f_X(x) \):**
Using the result from part (a), obtain the marginal probability density function of the random variable \( X \).
c) **Marginal Probability Density Function \( f_Y(y) \):**
Using the result from part (a), obtain the marginal probability density function of the random variable \( Y \).
d) **Verification of Functions:**
Verify the results of parts (b) and (c) to ensure that the two probability density functions are valid.
e) **Statistical Independence:**
Determine whether the two random variables are statistically independent.
f) **Expected Value \( E\{XY\} \):**
Obtain the expected value of the product \( XY \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F9328926a-b343-4d47-8a00-cbd9e6e36ac2%2Fafd82448-f5db-488f-82fa-4da35c6511b1%2F5einod6_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Joint Probability Density Function of Continuous Random Variables
The continuous random variables \( X \) and \( Y \) have a known joint probability density function \( f_{XY}(x, y) \) given by:
\[
f_{XY}(x, y) =
\begin{cases}
\frac{c \cdot x}{y + 1} & \text{if } 0 \leq y \leq x \leq 1 \\
0 & \text{otherwise}
\end{cases}
\]
where \( c \) is a positive constant.
#### Tasks:
a) **Determine the value of the constant \( c \):**
Find \( c \) such that the function becomes a valid joint probability density function.
b) **Marginal Probability Density Function \( f_X(x) \):**
Using the result from part (a), obtain the marginal probability density function of the random variable \( X \).
c) **Marginal Probability Density Function \( f_Y(y) \):**
Using the result from part (a), obtain the marginal probability density function of the random variable \( Y \).
d) **Verification of Functions:**
Verify the results of parts (b) and (c) to ensure that the two probability density functions are valid.
e) **Statistical Independence:**
Determine whether the two random variables are statistically independent.
f) **Expected Value \( E\{XY\} \):**
Obtain the expected value of the product \( XY \).
Expert Solution
Step 1: Continuous probability distribution
As per the guidelines of the Bartleby, solution of only first 3 parts are given.
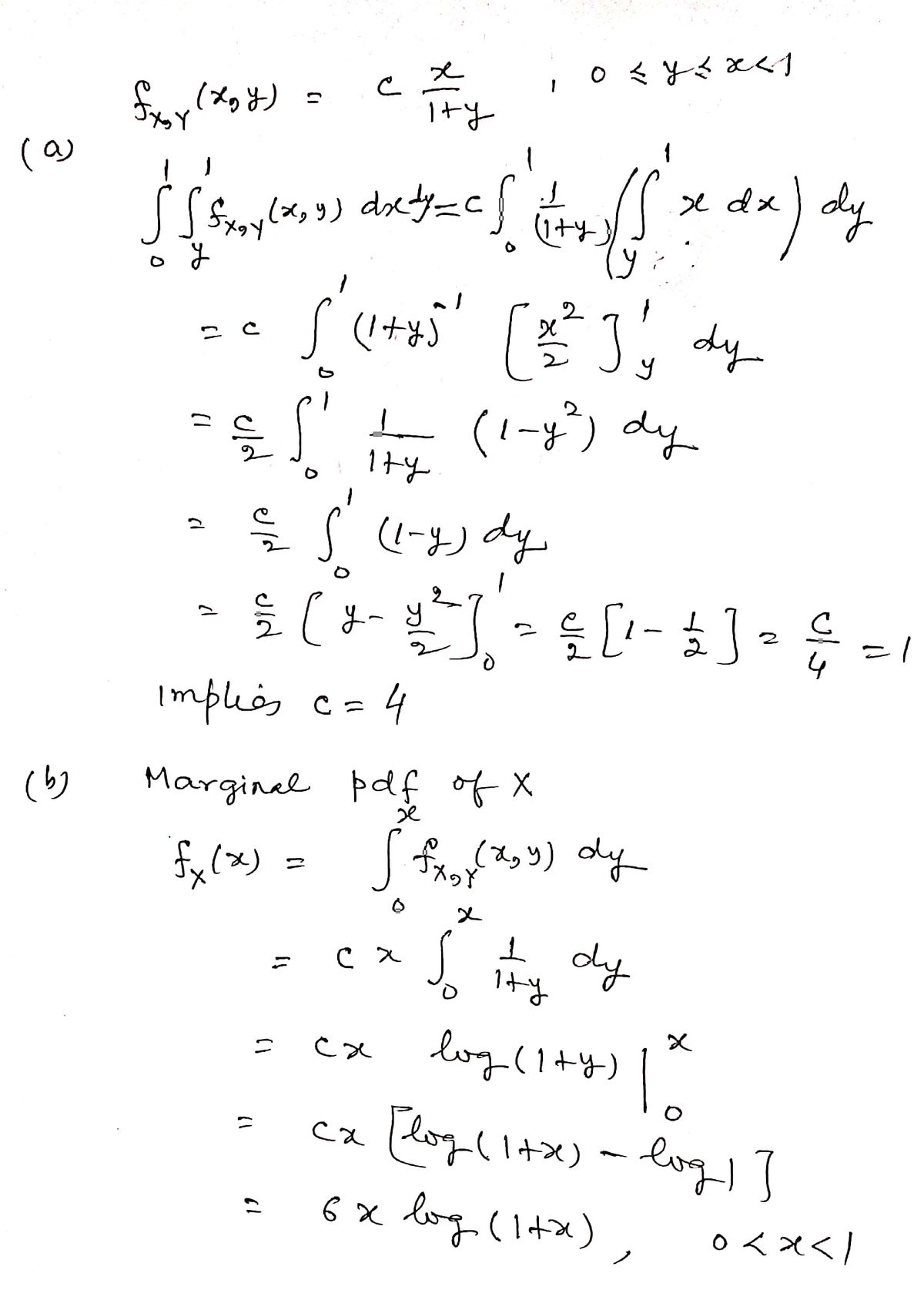
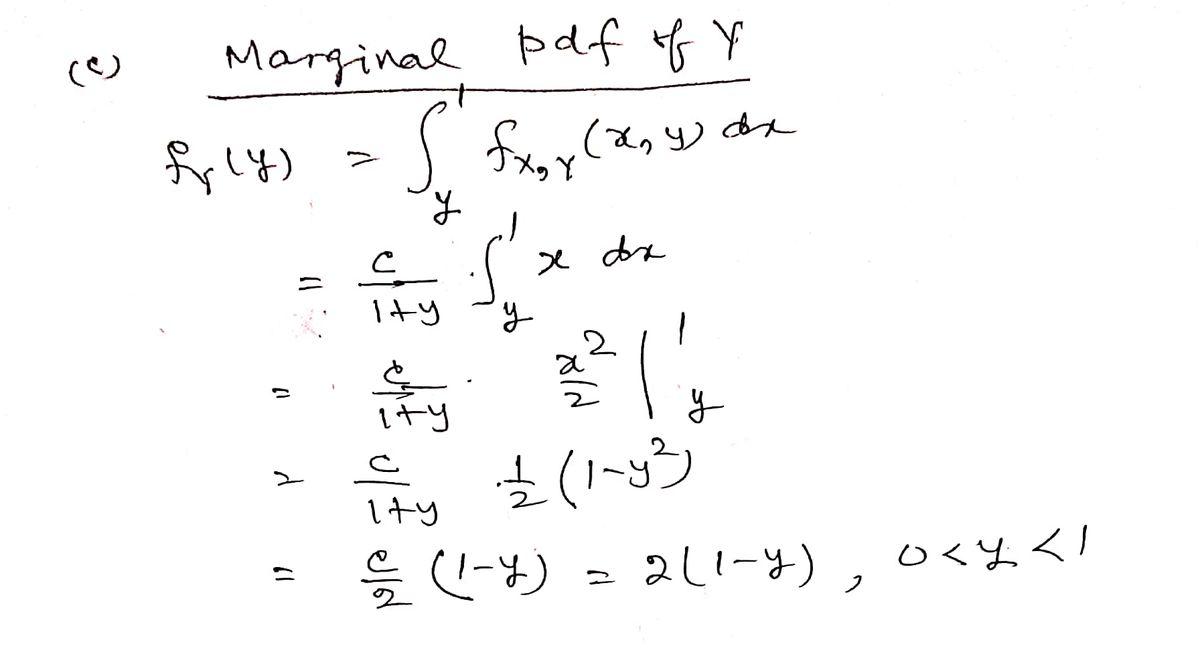
Step by step
Solved in 3 steps with 4 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
