Answered: Q4. The following data are from a…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Question

Q4. The following data are from a completely randomized design. At the α = 0.1, test whether the means for the three treatments are equal.

Need help with last 3 sub part questions please (B, C, D)

	Treatment 1	Treatment 2	Treatment 3
	34	40	42
	32	36	40
	35	43	48
	38	40	36
Sample mean	34.75	39.75	41.5
Sample variance	6.25	8.25	25

(A). What is the F test statistics value?

(a) 2.9312

(b) 4.9312

(d) 3.7278

(e) None of the above

(B). Using F table, what is the most possible range of values of the p-value?

(a) p-value>0.1

(b) 0.05<p-value<0.1

(d) 0.025<p-value<0.05

(e) None of the above

(C). What is the Fisher’s LSD value?

(a) 8.3449

(b) 4.7031

(d) 3.7449

(e) None of the above

(D). Is there a significant difference between the means for treatments 2 and 3?

(a) No, because 1.75<LSD

(b) Yes, because 1.75>LSD

(d) Yes, because 39.75≠41.5

(e) No, because 39.75<41.5

Expert Solution

Step 1

From the provided information , following table is obtained:

	Treatment 1	Treatment 2	Treatment 3
	34	40	42
	32	36	40
	35	43	48
	38	40	36

Sum =	139	159	166
Average =	34.75	39.75	41.5
$\sum_i X_{ij}^2 =$	4849	6345	6964
St. Dev. =	2.5	2.872	5
SS =	18.75	24.75	75
n =	4	4	4

The total sample size is $N = 12$ . Therefore, the total degrees of freedom are:

$d f_{t o t a l} = 12 - 1 = 11$

Also, the between-groups degrees of freedom are $df_{between} = 3 - 1 = 2$ , and the within-groups degrees of freedom are:

$df_{within} = df_{total} - df_{between} = 11 - 2 = 9$

Step 2

First, we need to compute the total sum of values and the grand mean. The following is obtained

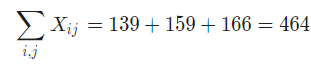
Also, the sum of squared values is

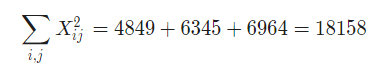
Based on the above calculations, the total sum of squares is computed as follows

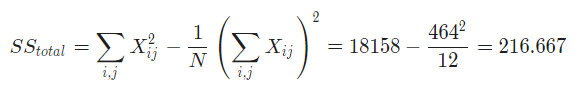
The within sum of squares is computed as shown in the calculation below:

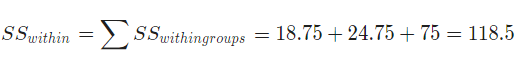
The between sum of squares is computed directly .
Now that sum of squares are computed, we can proceed with computing the mean sum of squares:

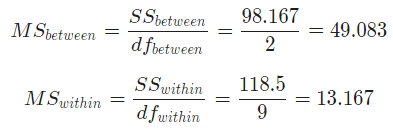
Finally, with having already calculated the mean sum of squares, the F-statistic is computed as follows:

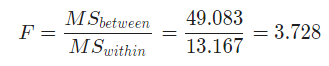
Step by step

Solved in 4 steps with 8 images

Knowledge Booster

$Anova and Design of Experiments$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Similar questions