Provide an appropriate response. The data below are the temperatures on randomly chosen days during the summer and the number of employee absences at a local company on those days. (a) Find the least square regression line. Round slope and y-intercept nearest hundredth. (b) Predict the number of absences when the temperature is 88. (c) Find the residual when the temperature is 98. Analyze the result.
Correlation
Correlation defines a relationship between two independent variables. It tells the degree to which variables move in relation to each other. When two sets of data are related to each other, there is a correlation between them.
Linear Correlation
A correlation is used to determine the relationships between numerical and categorical variables. In other words, it is an indicator of how things are connected to one another. The correlation analysis is the study of how variables are related.
Regression Analysis
Regression analysis is a statistical method in which it estimates the relationship between a dependent variable and one or more independent variable. In simple terms dependent variable is called as outcome variable and independent variable is called as predictors. Regression analysis is one of the methods to find the trends in data. The independent variable used in Regression analysis is named Predictor variable. It offers data of an associated dependent variable regarding a particular outcome.
Provide an appropriate response.
The data below are the temperatures on randomly chosen days during the summer and the number of employee absences at a local company on those days.
(a) Find the least square regression line. Round slope and y-intercept nearest hundredth.
(b) Predict the number of absences when the temperature is 88.
(c) Find the residual when the temperature is 98. Analyze the result.
(b) Test the claim, at the α = 0.05 level of significance, that a linear relation exists between the temperature and number of absences. Apply the classical approach and p-value approach.
(c) Find 95 % confidence interval about the slope fo the true least-square regression line. Interpret the result.

Since you have posted a question with multiple sub-parts, we will solve first three sub-
parts for you. To get remaining sub-part solved please repost the complete question and
mention the sub-parts to be solved.”
(a)
Use EXCEL to obtain the least-squares line.
EXCEL procedure:
- Go to EXCEL
- Go to Data>Data Analysis.
- Choose Regression.
- Input Y range as $B$1:$B$10.
- Input X range as $A$1:$A$10.
- Check the option Labels in First row.
- Click OK.
EXCEL output:
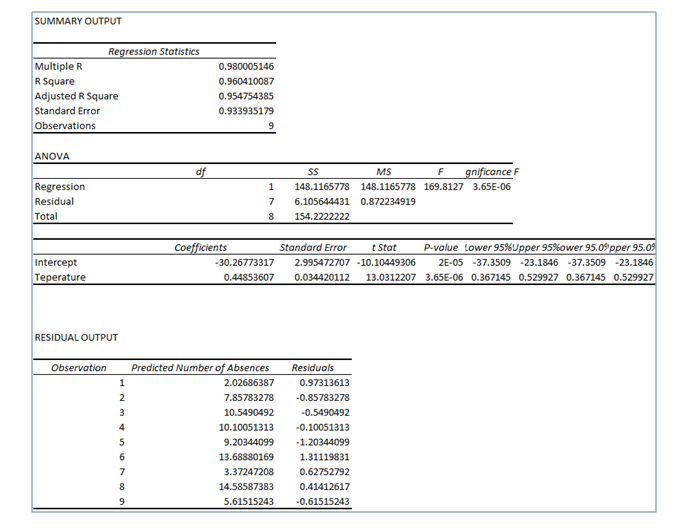
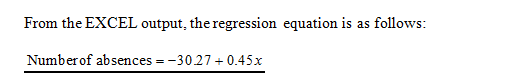
Thus, the value of slope is 0.45
The value of y intercept is –30.27.
Step by step
Solved in 2 steps with 2 images









