Prove that the following propositions are tautologies using rules of inference. a) ((p^q) ^ (pvq)) b) -(p-->q) --> p
Prove that the following propositions are tautologies using rules of inference. a) ((p^q) ^ (pvq)) b) -(p-->q) --> p
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Can you please help me prove that the following propositions in the first image attached are tautologies using the RULES OF INFERENCE!!! (which can be found in the second image I have attached)

Transcribed Image Text:Prove that the following propositions are tautologies using rules of inference.
a) -((p^q) ^ ~(pvq))
b) -(p-->q) --> p

Transcribed Image Text:itions: Logic and Proofs
TABLE 1 Rules of Inference.
Rule of Inference
P
P-9
:. 9
-q
P-9
קר .
P-9
9-r
.. pr
PV q
P
:.qu
P
:: pv q
p^ q
.. P
P
9
:. p^g
pv q
pvr
:: qvr
Tautology
(p^(p-q)) → 9
(-q ^ (p →q))
((p →q) ^ (q→r)) → (p → r)
→ P
-
((pvq) ^-p) → 9
P→ (pv q)
(p^q) → р
((p) ^ (q)) → (p^q)
((pvq) ^ (p Vr)) → (qvr)
This is an argument that uses the addition rule.
Name
Modus ponens
Modus tollens
Hypothetical syllogism
Disjunctive syllogism
Addition
Simplification
Conjunction
Resolution
LE 4 State which rule of inference is the basis of the following argument: "It is below
raining now. Therefore, it is below freezing now."
Solution: Let p be the proposition "It is below freezing now," and let q be the prop
raining now." This argument is of the form si botellons de l
on biley sus
to estu
Expert Solution
Step 1
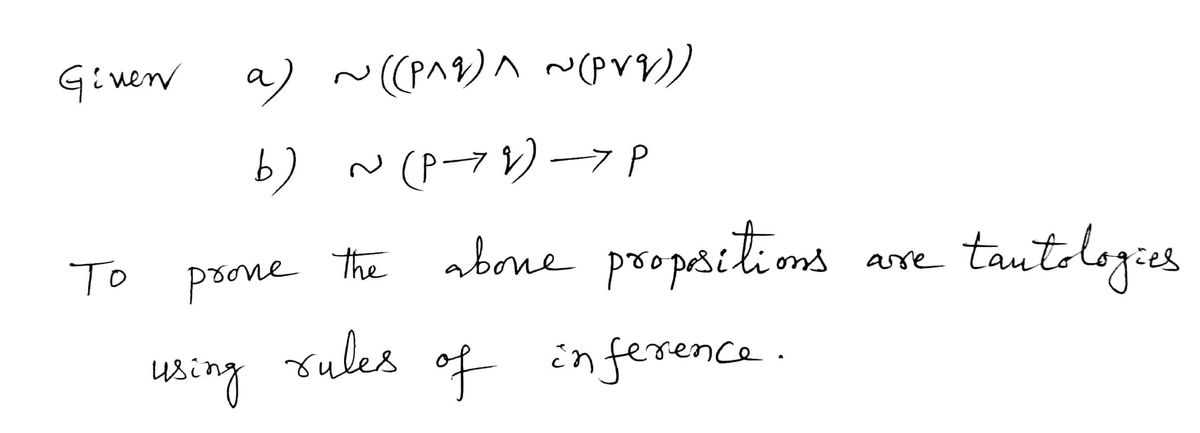
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

