Problem Statement: Any polar curve of the form r = f(0) can be parametrized using the parametric equations T = f(0) cos 0, y = f(8) sin 0 |(You may have noticed that the equations for r and y, respectively, are the equations x = r cos 0 and y = r sin 0, respectively, with r replaced by f(0).) (). dy d0 for the above parametrization of the polar curve r = f(0). (Hint: your (dx (a) Simplify de de 12 simplified answer should be in the form
Vector Arithmetic
Vectors are those objects which have a magnitude along with the direction. In vector arithmetic, we will see how arithmetic operators like addition and multiplication are used on any two vectors. Arithmetic in basic means dealing with numbers. Here, magnitude means the length or the size of an object. The notation used is the arrow over the head of the vector indicating its direction.
Vector Calculus
Vector calculus is an important branch of mathematics and it relates two important branches of mathematics namely vector and calculus.

Hi, thank you for the question. Since you have posted a question with multiple subpart, as per our policy we will answer only the first subpart. To get answers for other parts, kindly upload the question again specifying the parts to be solved.
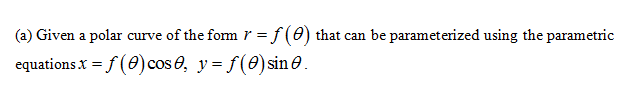
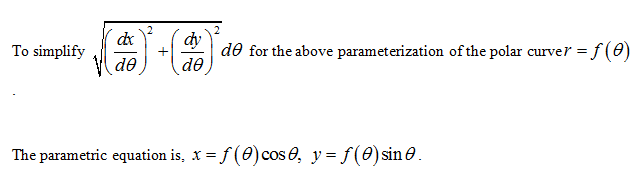

Step by step
Solved in 5 steps with 6 images









