Eliminate the parameter to (a simple!) Cartesian equation for the given parametric equations. Sketch the parametric curve and indicate the direction with arrows. x(1) = cos(1) y(t) = sec(1) 0 <1 < x/2
Eliminate the parameter to (a simple!) Cartesian equation for the given parametric equations. Sketch the parametric curve and indicate the direction with arrows. x(1) = cos(1) y(t) = sec(1) 0 <1 < x/2
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question

Transcribed Image Text:**Title: Converting Parametric Equations to Cartesian Form**
**Objective:**
To eliminate the parameter and derive a Cartesian equation from given parametric equations. Additionally, sketch the parametric curve and indicate the direction with arrows.
**Given Parametric Equations:**
- \( x(t) = \cos(t) \)
- \( y(t) = \sec(t) \)
**Interval:**
- \( 0 < t < \pi/2 \)
**Instructions:**
1. **Eliminate the Parameter \( t \):**
- Start with the identity \(\sec(t) = \frac{1}{\cos(t)}\).
- Replace \( y(t) \) using this identity: \( y = \sec(t) = \frac{1}{\cos(t)} \).
- Substitute \( x(t) = \cos(t) \) into \( y = \frac{1}{\cos(t)} \) to express \( y \) in terms of \( x \).
- The resulting equation is \( y = \frac{1}{x} \).
2. **Expression in Cartesian Coordinates:**
- **Cartesian Equation:** \( y = \frac{1}{x} \).
3. **Graphical Representation:**
- Sketch the curve based on the Cartesian equation \( y = \frac{1}{x} \).
- Indicate the direction of increasing \( t \) with arrows. As \( t \) increases from \( 0 \) to \(\pi/2\), \( x(t) = \cos(t) \) decreases from \( 1 \) to \( 0 \), while \( y(t) = \sec(t) \) increases from \( 1 \) to \( \infty \).
**Summary:**
This exercise demonstrates how to convert parametric equations to a Cartesian form, which can simplify graphing and analyzing the relationship between variables. The given curve represents a portion of the hyperbola \( y = \frac{1}{x} \) in the specified interval, highlighting the changing direction and behavior of the parametric equations as \( t \) varies.
Expert Solution
Step 1
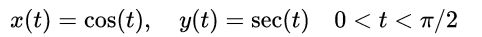
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning